
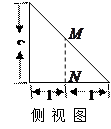
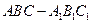 的直观图及其正视图、侧视图、俯视图如图所示.
的直观图及其正视图、侧视图、俯视图如图所示. 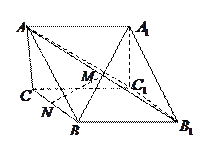

 面
面 ; (2)求点
; (2)求点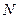 到平面
到平面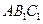 的距离;
的距离;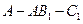 的大小.
的大小.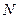 到平面
到平面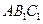 的距离
的距离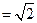 (3)二面角
(3)二面角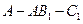 的平面角为
的平面角为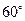 .
.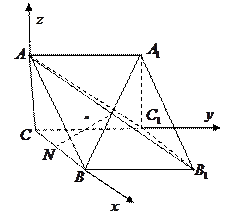
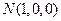 ,
,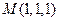 ,
,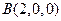
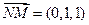 ,
, 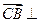 平面
平面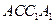 ,……………………1分
,……………………1分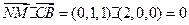 …………………………2分
…………………………2分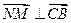 , ……………………… 3分
, ……………………… 3分 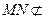 平面
平面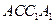
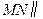 平面
平面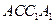 ………………………4分(或证明
………………………4分(或证明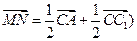
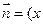 、
、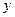 、
、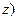 为平面
为平面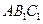 的法向量
的法向量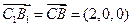
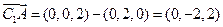
|
|
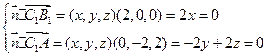 ∴取
∴取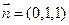 ………………………7分
………………………7分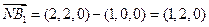
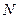 到平面
到平面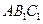 的距离
的距离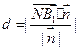
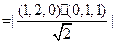
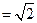 ……………9分
……………9分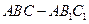 为直三棱柱,
为直三棱柱,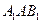 的法向量
的法向量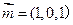 ………………………10分
………………………10分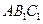 的法向量
的法向量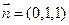
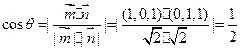 ……………………12分
……………………12分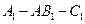 的大小为
的大小为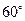 . ……………………13分
. ……………………13分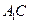 ,∵
,∵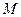 、
、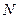 为
为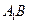 ,
,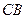 的中点,
的中点,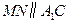 .
.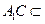 面
面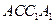
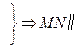 面
面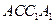
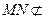 面
面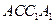
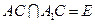 ,连接
,连接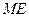 ,
,
|
|
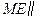
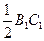 ,又
,又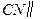
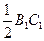 ,
,
|
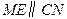 ,∴
,∴ .∵
.∵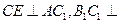 面
面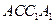 ,∴
,∴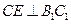
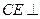 面
面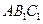 ,∴
,∴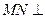 面
面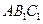 .
.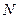 到平面
到平面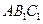 的距离
的距离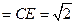 .
. 引
引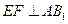 交
交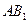 于
于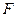 ,连接
,连接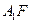 ,则
,则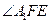 为二面角
为二面角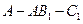 的平面角
的平面角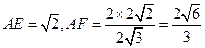
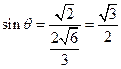 ,∴
,∴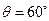 ∴二面角
∴二面角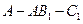 的平面角为
的平面角为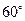 .
.

科目:高中数学 来源:不详 题型:解答题
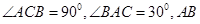 的垂直平分线分别交AB,AC于E,E(图一),沿DE将△ADE折起,使得平面ADE⊥平面BDEC(图二)
的垂直平分线分别交AB,AC于E,E(图一),沿DE将△ADE折起,使得平面ADE⊥平面BDEC(图二)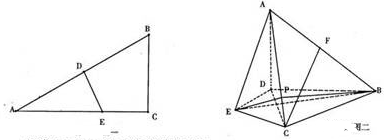
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
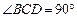 ,BC =" CD" = 1,AB⊥面BCD,
,BC =" CD" = 1,AB⊥面BCD,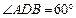 ,点E、F分别在AC、AD上,使面BEF⊥ACD,且EF∥CD,则平面BEF与平面BCD所成的二面角的正弦值为( )
,点E、F分别在AC、AD上,使面BEF⊥ACD,且EF∥CD,则平面BEF与平面BCD所成的二面角的正弦值为( )A.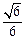 | B.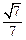 | C.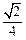 | D.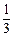 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
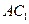 中
中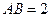 ,
,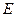 为
为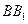 的中点.
的中点.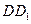 上确定一点F使
上确定一点F使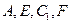 四点共面,并加以证明;
四点共面,并加以证明;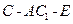 的平面角
的平面角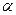 的余弦值;
的余弦值;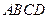 内,且点M在平面
内,且点M在平面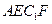 上的射影恰为
上的射影恰为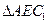 的重心,求异面直线
的重心,求异面直线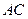 与
与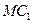 所成角的余弦值.
所成角的余弦值.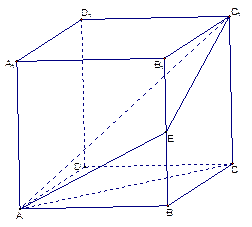
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
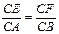 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).  | |||
 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com