设
，在平面直角坐标系中，已知向量
，
，动点
的轨迹为曲线
（Ⅰ）求曲线的方程，并说明该方程所表示曲线的形状；
（Ⅱ）已知
直线
与曲线交与不同的两点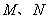
，则
的内切圆的面积是否存在最大值？若存在，求出这最大值及此时的实数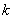
的值；若不存在，请说明理由．
中考利剑中考试卷汇编系列答案科目：高中数学 来源： 题型：
一个袋中有大小、质地相同的标号为
的三个小球.某人做如下游戏：每次从袋中摸一个小球，记下标号然后放回，共摸球
次.若拿出球的标号是奇数,则得
分,否则得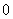
分，则次所得分数之和的数学期望是 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
对变量x，y有观测值(xi，yi)(i＝1,2，…，10)，得散点图①；对变量u，v有观测数据(ui，vi)(i＝1,2，…，10)，得散点图②.由这两个散点图可以判断( )
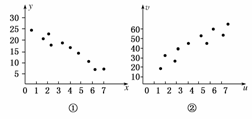A．变量x与y正相关，u与v正相关
B．变量x与y正相关，u与v负相关
C．变量x与y负相关，u与v正相关
D．变量x与y负相关，u与v负相关
查看答案和解析>>
科目：高中数学 来源： 题型：
命题：“若空间两条直线a，b分别垂直于平面α，则a∥b．”学生小夏这样证明：设a，b与面α分别相交于A，B，连接A，B．
∵a⊥α，b⊥α，AB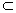
α，①
∴a⊥AB，b⊥AB，②
∴a∥b．③
这里的证明有两个推理，p：①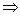
②，q：②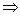③，则下列命题为真命题的是( )．
A．p∧q B．p∨q
C．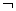
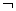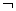p∨q D．(p)∧(q)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，即
时，方程表示两直线，方程为
； 
时，方程表示圆； 
时，方程表示椭圆； 
时，方程表示双曲线． 
，曲线
，
为其下焦点．
，则
，
，因此面积越大，
，不妨令
得
，则
，则
在
上单调递增
，
取得最大值3，又
，这时所求内切圆面积有最大值为
所求内切圆面积有最大值为
是定义在
上且以
为周期的奇函数,当
时,
,若函数
上的零点个数为
，则实数
的取值范围是_____________．
是双曲线
的左、右焦点，若点
关于直线
的对称点
也在双曲线上，则该双曲线的离心率为（ ）
B．
C．
D．
为
的重心，且
，则
的最大值为_________________．
，
则
( )
B.
