
分析 (1)由曲线C:$\left\{\begin{array}{l}{x=2cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数),利用平方关系可得C的普通方程.当$α=\frac{π}{3}$时,直线方程为:$\left\{\begin{array}{l}{x=2+\frac{1}{2}t}\\{y=\sqrt{3}+\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数),代入代入曲线C的普通方程,得13t2+56t+48=0,利用一元二次方程的根与系数的关系、弦长公式即可得出.
(2)将直线l的参数方程代入曲线C的普通方程,化为:(cos2α+4sin2α)t2+(8$\sqrt{3}$sinα+4cosα)t+12=0,利用根与系数的关系即可得出.
解答 解:(1)由曲线C:$\left\{\begin{array}{l}{x=2cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数),可得C的普通方程是$\frac{{x}^{2}}{4}+{y}^{2}$=1.
当$α=\frac{π}{3}$时,直线方程为:$\left\{\begin{array}{l}{x=2+\frac{1}{2}t}\\{y=\sqrt{3}+\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数),
代入曲线C的普通方程,得13t2+56t+48=0,
则线段AB的长度为$|AB|=|{t_1}-{t_2}|=\sqrt{{{({t_1}+{t_2})}^2}-4{t_1}{t_2}}=\sqrt{{{(-\frac{56}{13})}^2}-4×\frac{48}{13}}=\frac{{8\sqrt{10}}}{13}$.
(2)证明:将直线l的参数方程代入曲线C的普通方程,
化为:(cos2α+4sin2α)t2+(8$\sqrt{3}$sinα+4cosα)t+12=0,
∵$|PA|•|PB|=|{t_1}•{t_2}|=\frac{12}{{{{cos}^2}α+4{{sin}^2}α}}=\frac{{12({{cos}^2}α+{{sin}^2}α)}}{{{{cos}^2}α+4{{sin}^2}α}}=\frac{{12(1+{{tan}^2}α)}}{{1+4{{tan}^2}α}}$,
而直线的斜率为$\frac{\sqrt{5}}{4}$,则$tanα=\frac{{\sqrt{5}}}{4}$代入上式求得|PA|•|PB|=7.
又 $OP=\sqrt{{2^2}+{{({\sqrt{3}})}^2}}=\sqrt{7}$,
∴|PA|•|PB|=|OP|2.
点评 本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、直线与椭圆相交弦长问题、一元二次方程的根与系数,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
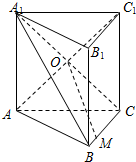 如图,已知直三棱柱ABC-A1B1C1的侧面ACC1A1是正方形,AC=BC,点O是侧面ACC1A1的中心,∠ACB=$\frac{π}{2}$,M在棱BC上,且MC=2BM=2.
如图,已知直三棱柱ABC-A1B1C1的侧面ACC1A1是正方形,AC=BC,点O是侧面ACC1A1的中心,∠ACB=$\frac{π}{2}$,M在棱BC上,且MC=2BM=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,1) | B. | (-2,1) | C. | (-∞,-2)∪(1,+∞) | D. | (-∞,-2]∪[1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com