
分析 (1)求出函数的导数,根据m的范围,判断导函数的符号,从而证明函数的单调性;
(2)求出函数的导数,通过讨论m的范围,求出函数的单调区间,从而判断函数的极值问题,求出m的具体范围.
解答 解:(1)函数定义域为(0,+∞),
$f'(m)=2x-2+\frac{m}{x}=\frac{{2{x^2}-2x+m}}{x}=\frac{{2{{(x-\frac{1}{2})}^2}+m-\frac{1}{2}}}{x}$,
所以$m≥\frac{1}{2}$时,对x∈(0,+∞),f'(x)≥0恒成立,
所以函数f(x)在定义域(0,+∞)上是增函数.
(2)由(1)知,当$m≥\frac{1}{2}$时,$f'(x)=\frac{{2{{(x-\frac{1}{2})}^2}+m-\frac{1}{2}}}{x}≥0$,
函数f(x)在(0,+∞)上是单调增函数,没有极值点.
当$m<\frac{1}{2}$时,令f'(x)=0得${x_1}=\frac{{1-\sqrt{1-2m}}}{2},{x_2}=\frac{{1+\sqrt{1-2m}}}{2}$,
①当m≤0时,${x_1}=\frac{{1-\sqrt{1-2m}}}{2}≤0$,
∴${x_1}∉(0,+∞),{x_2}=\frac{{1+\sqrt{1-2m}}}{2}≥1$,∴x2∈(0,+∞).
列表:
| x | (0,x2) | x2 | (x2,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 递减 | 极小值 | 极大值 |
| x | (0,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(β)<g(μ)<g(α)<g(λ) | B. | g(μ)<g(β)<g(λ)<g(α) | C. | g(α)<g(λ)<g(μ)<g(β) | D. | g(β)<g(μ)<g(λ)<g(α) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
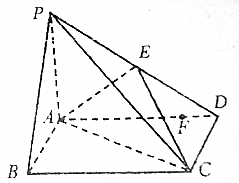 已知四棱锥P-ABCD中,PA⊥面ABCD,ABCD为矩形且PA=AB=2,AD=4,E为PD中点.
已知四棱锥P-ABCD中,PA⊥面ABCD,ABCD为矩形且PA=AB=2,AD=4,E为PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,12] | B. | [0,6] | C. | [0,12] | D. | [1,13] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com