
| A. | [-2,1) | B. | (-2,1) | C. | (-∞,-2)∪(1,+∞) | D. | (-∞,-2]∪[1,+∞) |
分析 设f(x)=x2+ax+2b,根据二次函数的性质与零点存在性定理可得f(0)>0、f(1)<0且f(2)>0.由此建立关于a、b的二元一次不等式组,设点E(a,b)为区域内的任意一点,根据直线的斜率公式可得k=$\frac{b-2}{a+2}$表示D、E连线的斜率,将点E在区域内运动并观察直线的倾斜角的变化,即可算出k的取值范围.
解答 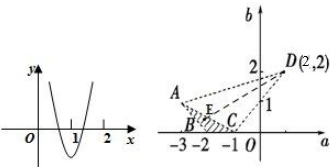 解:设f(x)=x2+ax+2b,
解:设f(x)=x2+ax+2b,
∵方程x2+ax+2b=0的一个根在区间(0,1)内,另一个根在区间(1,2)内,
∴可得$\left\{\begin{array}{l}{f(0)=2b>0}\\{f(1)=1+a+2b<0}\\{f(2)=4+2a+2b>0}\end{array}\right.$.
作出满足上述不等式组对应的点(a,b)所在的平面区域,
得到△ABC及其内部,即如图所示的阴影部分(不含边界).
其中A(-3,1),B(-2,0),C(-1,0),
设点E(a,b)为区域内的任意一点,
则k=$\frac{b-2}{a+2}$,表示点E(a,b)与点D(-2,2)连线的斜率.
∵KAD=1,kCD=-2,结合图形可知:KAD<k<KCD,
∴k的取值范围是(-2,1),
故选:B.
点评 本题着重考查了二次函数的性质、零点存在性定理、二元一次不等式组表示的平面区域、直线的斜率公式与两点间的距离公式等知识,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,12] | B. | [0,6] | C. | [0,12] | D. | [1,13] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π-2 | B. | $\frac{π}{2}$ | C. | $\frac{π}{4}$-$\frac{1}{2}$ | D. | $\frac{π}{2}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com