Question

5．已知函数f（x）=xlnx-$\frac{a}{2}$x²-x+a（a∈R）在其定义域内有两个不同的极值点，则实数a的取值范围是（0，$\frac{1}{e}$）．

Answer 1

分析 由导数与极值的关系知可转化为方程f′（x）=lnx-ax=0在（0，+∞）有两个不同根；再转化为函数y=lnx与函数y=ax的图象在（0，+∞）上有两个不同交点，通过函数的导数利用曲线的斜率，从而求解a的范围；

解答 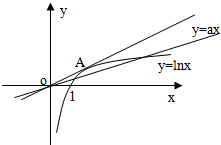解：由题意知，函数f（x）的定义域为（0，+∞），
方程f′（x）=0在（0，+∞）有两个不同根；
即方程lnx-ax=0在（0，+∞）有两个不同根；
转化为函数y=lnx与函数y=ax的图象在（0，+∞）上有两个不同交点，
如右图．
可见，若令过原点且切于函数y=lnx图象的直线斜率为k，
只须0＜a＜k．
令切点A（x₀，lnx₀），
故k=y′${|}_{x={x}_{0}}^{\;}$=$\frac{1}{{x}_{0}}$，又k=$\frac{ln{x}_{0}}{{x}_{0}}$，
故$\frac{1}{{x}_{0}}$=$\frac{ln{x}_{0}}{{x}_{0}}$，
解得，x₀=e，
故k=$\frac{1}{e}$，
故0＜a＜$\frac{1}{e}$．
故答案为：（0，$\frac{1}{e}$）．

点评 本题考查了导数的综合应用，转化思想，数形结合的思想方法的应用，属于中档题．