
分析 分别说明两个不等式表示的区域;讨论x∈[-1,0)与x∈[0,1)和x∈[1,2)时,化简集合B,求出所表示的平面区域所对应的面积.
解答 解:不等式y≤k(x-$\frac{1}{2}$)+$\frac{1}{2}$,k∈R,表示的区域为整个平面,而
不等式[x]2+[y]2≤1,当0≤x<1,0≤y<1时,[x]=0,[y]=0,满足条件[x]2+[y]2≤1;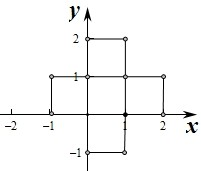
当0≤x<1,1≤y<2时,[x]=0,[y]=1,满足条件[x]2+[y]2≤1;
当0≤x<1,-1≤y<0时,[x]=0,[y]=-1,满足条件[x]2+[y]2≤1;
当-1≤x<0,0≤y<1时,[x]=-1,[y]=0满足条件[x]2+[y]2≤1;
当0≤y<1,1≤x<2时,[x]=0,[y]=1满足条件[x]2+[y]2≤1;
∴满足条件[x]2+[y]2≤1的点(x,y)构成的平面区域是五个边长为1的正方形,如图,其面积为:5
所以不等式组表示的区域面积为5;
故答案为:5.
点评 本题考查了不等式表示平面区域的应用问题,也考查了分类讨论思想的应用问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
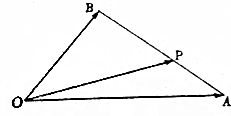 如图,在△OAB中,已知P为线段AB上的一点.|$\overrightarrow{OA}$|=4,|$\overrightarrow{OB}$|=3,且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°.
如图,在△OAB中,已知P为线段AB上的一点.|$\overrightarrow{OA}$|=4,|$\overrightarrow{OB}$|=3,且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com