练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图2-4-19,BC为⊙O直径,DE切⊙O于A点,BD⊥DE于D,若∠ABD=50°,则的度数为_________________.

    图2-4-19

    解析:∵BD⊥DE,

    ∴∠BDA=90°.

    ∴∠ABD+∠BAD=90°.

    ∴∠BAD=90°-50°=40°.

    ∵AB是弦,AD是切线,

    ∴∠C=∠BAD=40°.

    ∴BC是直径.∴∠BAC=90°.

    ∴∠C+∠ABC=90°.

    ∴∠ABC=90°-∠C=50°.

    ∴的度数为100°.

    答案:100°

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，在平面直角坐标系xoy中，以O为顶点，x轴正半轴为始边作两个锐角α，β，它们的终边分别与单位圆相
    交于A、B两点，已知A、B的横坐标分别为
    		2
    10
    ，
    2
    		5
    5
    ．
    （1）求tan(-
    19π
    4
    +α+β)    的值；
    （2）求α+2β的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

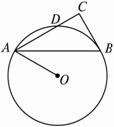
    如图19,点A、B为⊙O上两点,经过点B的切线BC与过点A的弦AD的延长线交于点C,∠DAB =∠OAB,BC =4,CD =2,则AB =           .

    图19

    查看答案和解析>>

    科目：高中数学 来源： 题型：

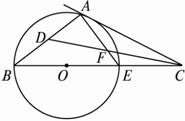
    如图2-4-19,已知C点在⊙O直径BE的延长线上,CA切⊙O于A点,∠BAC的平分线交AE于F点,∠BCA的平分线交AB于D点.

    图2-4-19

    (1)求∠ADF的度数.

    (2)若∠ACB的度数为y度,∠B的度数为x度,那么y与x之间有怎样的关系？试写出你的猜测并给出证明.

    (3)若AB =AC,求AC∶BC.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，ABCD是边长为2的正方形纸片，沿某动直线Z为折痕将正方形在其下方的部分向上翻折，使得每次翻折后点B都落在边AD上，记为B′；折痕l与AB交于点E，点M满足关系式．

    (1)建立适当的直角坐标系，求点M的轨迹方程；

    (2)若曲线C是由点M的轨迹及其关于边AB对称的曲线组成的，F是AB边上的一点，=4，过点F的直线交曲线C于P、Q两点，且，求实数A的取值范围．

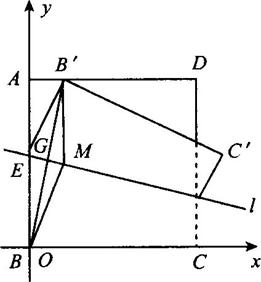
    第19题图

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (理)如图a所示，某地为了开发旅游资源，欲修建一条连接风景点P和居民区O的公路，点P所在的山坡面与山脚所在水平面α所成的二面角为θ(0°＜θ＜90°)，且sinθ=，点P到平面α的距离PH=0．4(km)．沿山脚原有一段笔直的公路AB可供利用．从点O到山脚修路的造价为a万元／km，原有公路改建费用为万元／km．当山坡上公路长度为l km(1≤l≤2)时，其造价为(l2+1)a万元已知OA⊥AB，PB⊥AB，AB=1．5(km)，OA=(km)．

    (1)在AB上求一点D，使沿折线PDAO修建公路的总造价最小；

    (2)对于(1)中得到的点D，在DA上求一点E，使沿折线PDEO修建公路的总造价最小；

    (3)在AB上是否存在两个不同的点D′，E′，使沿折线．PD′E′O修建公路的总造价小于(2)中得到的最小总造价?证明你的结论．

    a)

    第19题图

    (文)如图b所示，直四棱柱ABCD-A1B1C1D1中，∠ADC=90°，△ABC为等边三角形，且AA1=AD=DC=2．

    (1)求AC1与BC所成角的余弦值；

    (2)求二面角C1-BD-C的大小；

    (3)设M是BD上的点，当DM为何值时，D1M⊥平面A1C1D?并证明你的结论．

    第19题图

    查看答案和解析>>

    同步练习册答案