
已知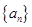 是公比为
是公比为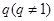 的等比数列,且
的等比数列,且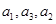 成等差数列.
成等差数列.
⑴求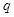 的值;
的值;
⑵设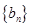 是以
是以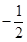 为首项,
为首项,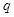 为公差的等差数列,求
为公差的等差数列,求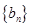 的前
的前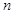 项和
项和 .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
设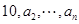 是各项均不为零的
是各项均不为零的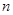 (
(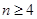 )项等差数列,且公差
)项等差数列,且公差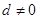 .
.
(1)若 ,且该数列前
,且该数列前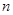 项和
项和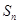 最大,求
最大,求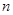 的值;
的值;
(2)若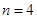 ,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求
,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求 的值;
的值;
(3)若该数列中有一项是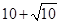 ,则数列
,则数列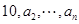 中是否存在不同三项(按原来的顺序)为等比数列?请说明理由.
中是否存在不同三项(按原来的顺序)为等比数列?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了保障幼儿园儿童的人身安全,国家计划在甲、乙两省试行政府规范购置校车方案,计划若干时间内(以月为单位)在两省共新购1000辆校车.其中甲省采取的新购方案是:本月新购校车10辆,以后每月的新购量比上一月增加50%;乙省采取的新购方案是:本月新购校车40辆,计划以后每月比上一月多新购m辆.
(1)求经过n个月,两省新购校车的总数S(n);
(2)若两省计划在3个月内完成新购目标,求m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列{an},其前n项和为Sn.
(1)若对任意的n∈N,a2n-1,a2n+1,a2n组成公差为4的等差数列,且a1=1,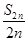 =2013,求n的值;
=2013,求n的值;
(2)若数列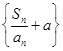 是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+
是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+ .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知等差数列{an}前三项之和为-3,前三项积为8.
(1)求等差数列{an}的通项公式;
(2)若a2,a3,a1成等比数列,求数列{|an|}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知等差数列{an}中,a2+a4=10,a5=9,数列{bn}中,b1=a1,bn+1=bn+an.
(1)求数列{an}的通项公式,写出它的前n项和Sn.
(2)求数列{bn}的通项公式.
(3)若cn= ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com