
【题目】已知曲线![]() 上的点到点
上的点到点![]() 的距离比它到直线
的距离比它到直线![]() 的距离小2.
的距离小2.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
, ![]() 两点,若
两点,若![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
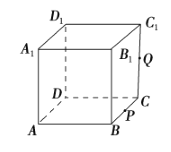
【题目】如图,正方体![]() 的棱长为 1,
的棱长为 1, ![]() 为
为![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点,过点A、P、Q的平面截该正方体所得的截面记为
上的动点,过点A、P、Q的平面截该正方体所得的截面记为![]() .则下列命题正确的是__________(写出所有正确命题的编号).
.则下列命题正确的是__________(写出所有正确命题的编号).
①当![]() 时,
时, ![]() 为四边形;②当
为四边形;②当![]() 时,
时, ![]() 为等腰梯形;③当
为等腰梯形;③当![]() 时,
时, ![]() 为六边形;④当
为六边形;④当![]() 时,
时, ![]() 的面积为
的面积为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M是圆心为E的圆![]() 上的动点,点
上的动点,点![]() ,线段MF的垂直平分线交EM于点P.
,线段MF的垂直平分线交EM于点P.
(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)过原点O作直线交(Ⅰ)中轨迹C于点A、B,点D满足![]() ,试求四边形AFBD的面积的取值范围.
,试求四边形AFBD的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC
(1)求三棱锥D-ABC的体积
(2)求证:平面DAC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=![]() CA,求证:MN∥平面DEF
CA,求证:MN∥平面DEF

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知坐标平面上点![]() 与两个定点
与两个定点![]() ,
, ![]() 的距离之比等于5.
的距离之比等于5.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为![]() ,过点
,过点![]() 的直线
的直线![]() 被
被![]() 所截得的线段的长为8,求直线
所截得的线段的长为8,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得![]() =80,
=80, ![]() =20,
=20, ![]() =184,
=184, ![]() =720.
=720.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中,  ,a=
,a=![]() -b
-b![]() ,其中
,其中![]() ,
, ![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com