
【题目】在各项均为正数的等比数列![]() 中,
中, ![]() ,且
,且![]() 成等差数列.
成等差数列.
(1)求等比数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)当n=5时,Tn的最大值为25.
;(2)当n=5时,Tn的最大值为25.
【解析】试题分析:(1)设数列![]() 的公比为
的公比为![]() ,由等差中顶和等比数列的通项公式列出方程组,结合题意求出
,由等差中顶和等比数列的通项公式列出方程组,结合题意求出![]() 的值,再代入等比数列的通项公式化简即可;(2)由(1)和题意化简
的值,再代入等比数列的通项公式化简即可;(2)由(1)和题意化简![]() ,并判断出数列
,并判断出数列![]() 是等差数列,求出首项和公差,代入等差数列的前
是等差数列,求出首项和公差,代入等差数列的前![]() 项和公式,再对
项和公式,再对![]() 进行配方,根据二次函数的性质求出它的最大值.
进行配方,根据二次函数的性质求出它的最大值.
试题解析:(1)设数列{an}的公比为q,an>0
因为2a1,a3,3a2成等差数列,
所以2a1+3a2=2a3,
即![]() ,
,
所以2q2-3q-2=0,
解得q=2或![]() (舍去),
(舍去),
又a1=2,所以数列{an}的通项公式![]() .
.
(2)由题意得,bn=11-2log2an=11-2n,
则b1=9,且bn+1-bn=-2,
故数列{bn}是首项为9,公差为-2的等差数列,
所以![]() =-(n-5)2+25,
=-(n-5)2+25,
所以当n=5时,Tn的最大值为25.


科目:高中数学 来源: 题型:
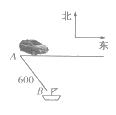
【题目】如图所示,一辆汽车从![]() 市出发沿海岸一条直公路以
市出发沿海岸一条直公路以![]() 的速度向东匀速行驶,汽车开动时,在
的速度向东匀速行驶,汽车开动时,在![]() 市南偏东30°方向距
市南偏东30°方向距![]() 市
市![]() 的海上
的海上![]() 处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.问快艇至少以多大的速度,以什么样的航向行驶才能最快把稿件送到司机手中?
处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.问快艇至少以多大的速度,以什么样的航向行驶才能最快把稿件送到司机手中?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题,其中正确的个数有( )
①由独立性检验可知,有![]() 的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
②两个随机变量相关性越强,则相关系数的绝对值越接近于1;
③在线性回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加0.2个单位;
平均增加0.2个单位;
④对分类变量![]() 与
与![]() ,它们的随机变量
,它们的随机变量![]() 的观测值
的观测值![]() 来说,
来说, ![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一条光线经过P(2,3)点,射在直线l:x+y+1=0上,反射后穿过点Q(1,1).
(1)求入射光线的方程;
(2)求这条光线从P到Q的长度.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C: ![]() ,点
,点![]() 在x轴的正半轴上,过点M的直线
在x轴的正半轴上,过点M的直线![]() 与抛物线C相交于A,B两点,O为坐标原点.
与抛物线C相交于A,B两点,O为坐标原点.
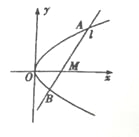
(1)若![]() ,且直线
,且直线![]() 的斜率为1,求以AB为直径的圆的方程;
的斜率为1,求以AB为直径的圆的方程;
(2)是否存在定点M,使得不论直线![]() 绕点M如何转动,
绕点M如何转动, ![]() 恒为定值?
恒为定值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中心在坐标原点,焦点在坐标轴上,且经过
中心在坐标原点,焦点在坐标轴上,且经过![]() 三点.
三点.
(1)求椭圆![]() 的方程;
的方程;
(2)在直线![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,分别与椭圆
,分别与椭圆![]() 交于
交于![]() 两点,判断直线
两点,判断直线![]() 是否过定点?若是,求出该定点.若不是,请说明理由.
是否过定点?若是,求出该定点.若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() .
.
(1)若![]() 分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6),先后抛掷两次时第一次、第二次出现的点数,求满足
分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6),先后抛掷两次时第一次、第二次出现的点数,求满足![]() 的概率;
的概率;
(2)若![]() 在连续区间
在连续区间![]() 上取值,求满足
上取值,求满足![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com