Question

19．如图，在平面直角坐标系xOy中，设a₁=2，有一组圆心在x轴正半轴上的圆A_n（n=1，2，…）与x轴的交点分别为A₀（1，0）和A_n+1（a_n+1，0），过圆心A_n作垂直于x轴的直线l_n，在第一象限与圆A_n交于点B_n（a_n，b_n）
（Ⅰ）试求数列{a_n}的通项公式
（Ⅱ）设曲边形A_n+1B_nB_n+1（阴影所示）的面积为S_n，若对任意n∈N^*，$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+…+$\frac{1}{{S}_{n}}$≤m恒成立，试求实数m的取值范围．

Answer 1

分析 （Ⅰ）由条件可得a_n+1-1=2（a_n-1），所以数列{a_n-1}是等比数列，从而${a}_{n}={2}^{n-1}+1$；
（Ⅱ）由（Ⅰ）可得各点坐标为B_n（2^n-1+1，2^n-1），B_n+1（2ⁿ+1，2ⁿ），且${A}_{n}（{2}^{n-1}+1，0）$，${A}_{n+1}（{2}^{n}+1，0）$，从而${S}_{n}={S}_{梯形{A}_{n}{B}_{n}{B}_{n+1}{A}_{n+1}}$-${S}_{扇形{A}_{n}{B}_{n}{A}_{n+1}}$，计算可得$\frac{1}{{S}_{n}}=\frac{4}{6-π}•（\frac{1}{4}）^{n-1}$，从而$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+…+$\frac{1}{{S}_{n}}$=$\frac{16}{18-3π}[1-（\frac{1}{4}）^{n}]$，所以实数m≥$\frac{16}{18-3π}$．

解答 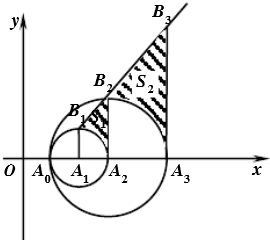解：（Ⅰ）由条件可得，a_n+1-1=2（a_n-1），
∴数列{a_n-1}是等比数列．
又∵a₁-1=1，
所以${a}_{n}-1={2}^{n-1}$，
${a}_{n}={2}^{n-1}+1$；
（Ⅱ）∵b_n=${a}_{n}-1={2}^{n-1}$，
∴B_n（2^n-1+1，2^n-1），
∴B_n+1（2ⁿ+1，2ⁿ），且${A}_{n}（{2}^{n-1}+1，0）$，${A}_{n+1}（{2}^{n}+1，0）$，
${S}_{n}={S}_{梯形{A}_{n}{B}_{n}{B}_{n+1}{A}_{n+1}}$-${S}_{扇形{A}_{n}{B}_{n}{A}_{n+1}}$
=$\frac{1}{2}×{2}^{n-1}×（{2}^{n-1}+{2}^{n}）$-$\frac{1}{4}π×（{2}^{n-1}）^{2}$
=$\frac{6-π}{4}×{4}^{n-1}$，
所以$\frac{1}{{S}_{n}}=\frac{4}{6-π}•（\frac{1}{4}）^{n-1}$，
所以$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+…+$\frac{1}{{S}_{n}}$=$\frac{4}{6-π}[1+\frac{1}{4}+…+（\frac{1}{4}）^{n-1}]$
=$\frac{4}{6-π}•\frac{1-（\frac{1}{4}）^{n}}{1-\frac{1}{4}}$
=$\frac{16}{18-3π}[1-（\frac{1}{4}）^{n}]$
＜$\frac{16}{18-3π}$，
故可得实数m≥$\frac{16}{18-3π}$．

点评 本题考查了递推式的应用，面积的求法，考查了推理能力与计算能力，属于难题．