
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
-1-
| ||
| a |
-1+
| ||
| a |
-1-
| ||
| a |
-1+
| ||
| a |
-1-
| ||
| a |
-1+
| ||
| a |
-1+
| ||
| a |
-1-
| ||
| a |


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源:不详 题型:单选题
| A.(-1,1) | B.(-1,0)∪(2,3) |
| C.(-∞,-1)∪(2,3) | D.(-∞,-1)∪(0,2)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
|
| A.{x|-1<x<1} | B.{x|0<x<3} | C.{x|0<x<1} | D.{x|-1<x<3} |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
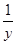 ,b=y+
,b=y+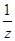 ,c=z+
,c=z+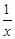 ,则a,b,c三数
,则a,b,c三数| A.至少有一个不大于2 | B.都小于2 |
| C.至少有一个不小于2 | D.都大于2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
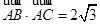 ,∠BAC=30°,设M是△ABC内的一点(不在边界上),定义f(M)=(x,y,z),其中
,∠BAC=30°,设M是△ABC内的一点(不在边界上),定义f(M)=(x,y,z),其中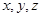 分别表示△MBC,△MCA,△MAB的面积,若
分别表示△MBC,△MCA,△MAB的面积,若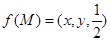 ,则
,则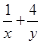 的最小值为__________________
的最小值为__________________查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com