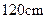练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    用边长为的正方形铁皮做一个无盖水箱，先在四角分别截去一个小正方形，然后把四边翻转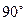角，再焊接成水箱．问：水箱底边的长取多少时，水箱容积最大？最大容积是多少？
    水箱底边长取时，容积最大．其最大容积为
    设水箱底边长为，则水箱高为．
    水箱容积．
    ．
    令，得（舍）或．
    当在内变化时，导数的正负如下表：





    		＋

    		－
    因此在处，函数取得极大值，并且这个极大值就是函数的最大值．
    将代入，得最大容积．
    答：水箱底边长取时，容积最大．其最大容积为．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    设函数＝是奇函数，其中，，。
    （Ⅰ）求的值；
    （Ⅱ）判断并证明在上的单调性。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知函数的图像在点处的切线方程为．
    （Ⅰ）求函数的解析式；  （Ⅱ）求函数的单调区间．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

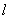    某人在一山坡P处观看对面山项上的一座铁塔，如图所示，塔高BC=80（米），塔所在的山高OB=220（米），OA=200（米），图中所示的山坡可视为直线l且点P在直线上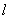，与水平地面的夹角为a ,tana=1/2试问此人距水平地面多高时，观看塔的视角∠BPC最大（不计此人的身高）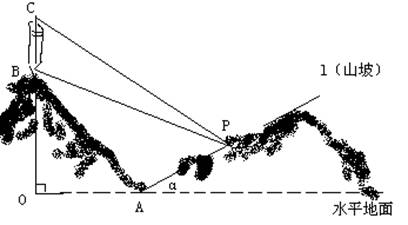

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

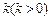    某银行准备新设一种定期存款业务，经预测，存款量与利率的平方成正比，比例系数为，且知当利率为0.012时，存款量为1.44亿；又贷款的利率为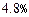时，银行吸收的存款能全部放贷出去；若设存款的利率为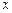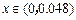，，则当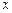为多少时，银行可获得最大收益？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    设函数，点An为函数y＝f（x）图象上横坐标为n（n∈N*）的点，O为坐标原点，向量e＝(1，0)。记为向量与e的夹角，，则       ；     。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    有一个长度为5 m的梯子贴靠在笔直的墙上，假设其下端沿地板以3 m/s的速度离开墙脚滑动，求当其下端离开墙脚1.4 m时，梯子上端下滑的速度.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

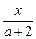    已知对于x的所有实数值，二次函数f(x)=x2－4ax+2a+12(a∈R)的值都是非负的，求关于x的方程=|a－1|+2的根的取值范围.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    路灯距地平面为,一个身高为的人以的速率在地面上行走，从路灯在地平面上射影点C，沿某直线离开路灯，求人影长度的变化速率v.

    查看答案和解析>>

    同步练习册答案