
【题目】如图,在直角梯形ABCD中AD∥BC,∠ADC=90°,平面ABCD外一点P在平面ABCD内的射影Q恰在边AD上, PA=AD=2 BC=2,CD=.
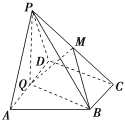
(1)若平面PQB⊥平面PAD,求证:Q为线段AD中点;
(2)在(1)的条件下,若M在线段PC上,且PA∥平面BMQ,求点M到平面PAB的距离.
【答案】(1)见解析;(2)![]()
【解析】(1)证明:∵P在平面ABCD内的射影Q恰在边AD上,
∴PQ⊥平面ABCD,
∵BQ![]() 平面ABCD,∴PQ⊥BQ,(2分)
平面ABCD,∴PQ⊥BQ,(2分)
∵PQB⊥平面PAD,且平面PQB∩平面PAD =PQ,
∴BQ⊥平面PAD.
∵AD![]() 平面PAD,∴BQ⊥AD.(4分)
平面PAD,∴BQ⊥AD.(4分)
∵∠ADC=90°,∴CD∥BQ,
又AD∥BC,∴四边形BCDQ为平行四边形,
∴BC=QD=1,AQ=AD-QD=2-1=1,
∴AQ=QD,即Q为线段AD中点.(6分)
(2)连接AC与BQ交于点N,则N为AC中点,连接![]() ,
,
∵PA∥平面BMQ,∴PA∥MN,
∴M为PC中点,(8分)
∴点M到平面PAB的距离是点C到平面PAB的距离的![]() ,
,
在三棱锥![]() 中,高
中,高![]() ,底面积为
,底面积为![]() ,
,
∴三棱锥![]() 的体积
的体积![]() ,(10分)
,(10分)
又△PAB中,PA=AB=2,PB=![]() ,
,
∴△PAB的面积为![]() .
.
设点M到平面PAB的距离为d,由![]() 可得
可得![]() ,则
,则![]() ,
,
∴点M到平面PAB的距离为![]() .(12分)
.(12分)


科目:高中数学 来源: 题型:
【题目】如图,过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() 分别作直线
分别作直线![]() ,
, ![]() 交椭圆于
交椭圆于![]() 与
与![]() ,且
,且![]() .
.
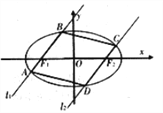
(1)求证:当直线![]() 的斜率
的斜率![]() 与直线
与直线![]() 的斜率
的斜率![]() 都存在时,
都存在时, ![]() 为定值;
为定值;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣4,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某商品的进货单价为1元/件,商户甲往年以单价2元/件销售该商品时,年销量为1万件.今年拟下调销售单价以提高销量增加收益.据估算,若今年的实际销售单价为![]() 元/件(
元/件(![]() ),则新增的年销量
),则新增的年销量![]() (万件).
(万件).
(1)写出今年商户甲的收益![]() (单位:万元)与
(单位:万元)与![]() 的函数关系式;
的函数关系式;
(2)商户甲今年采取降低单价提高销量的营销策略,是否能获得比往年更大的收益(即比往年收益更多)?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两企业生产同一种型号零件,按规定该型号零件的质量指标值落在![]() 内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
甲企业:

乙企业:

(1)已知甲企业的500件零件质量指标值的样本方差![]() ,该企业生产的零件质量指标值
,该企业生产的零件质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为质量指标值的样本平均数
近似为质量指标值的样本平均数![]() (注:求
(注:求![]() 时,同一组数据用该区间的中点值作代表),
时,同一组数据用该区间的中点值作代表),![]() 近似为样本方差
近似为样本方差![]() ,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
(2)由以上统计数据完成下面![]() 列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.

附注:
参考数据: ![]() ,
,
参考公式: ![]() ,
, ![]() ,
,
![]() .
.
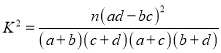
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校歌咏比赛中,甲班、乙班、丙班、丁班均可从![]() 、
、![]() 、
、![]() 、
、![]() 四首不同曲目中任选一首.
四首不同曲目中任选一首.
(1)求甲、乙两班选择不同曲目的概率;
(2)设这四个班级总共选取了![]() 首曲目,求
首曲目,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点.
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在多面体![]() 中,四边形
中,四边形![]() 与四边形
与四边形![]() 均为边长为2的正方形,
均为边长为2的正方形,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
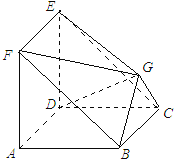
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求多面体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com