
【题目】已知函数f(x)=ln x-![]() .
.
(1)试讨论f(x)在定义域上的单调性;
(2)若f(x)在[1,e]上的最小值为![]() ,求a的值.
,求a的值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)由题得f(x)的定义域为(0,+∞),且![]() .分类讨论可得:当a≥0时,f(x)在(0,+∞)上是单调递增函数.当a<0时,f(x)在(0,-a]上为减函数,在(-a,+∞)上为增函数.
.分类讨论可得:当a≥0时,f(x)在(0,+∞)上是单调递增函数.当a<0时,f(x)在(0,-a]上为减函数,在(-a,+∞)上为增函数.
(2)由(1)可知: ![]() ,分类讨论:①若a≥-1,f(x)min=f(1),可得
,分类讨论:①若a≥-1,f(x)min=f(1),可得![]() ,不合题意;②若a≤-e,f(x)min=f(e),可得
,不合题意;②若a≤-e,f(x)min=f(e),可得![]() ,不合题意;③若-e<a<-1,f(x)min=f(-a),可得
,不合题意;③若-e<a<-1,f(x)min=f(-a),可得![]() ,符合题意.
,符合题意.
试题解析:
(1)由题得f(x)的定义域为(0,+∞),且f′(x)=![]() +
+![]() =
=![]() .
.
当a≥0时,f′(x)>0,故f(x)在(0,+∞)上是单调递增函数.
当a<0时,由f′(x)=0得x=-a,由f′(x)>0得,x>-a,由f′(x)<0得,x<-a,
∴当a<0时,f(x)在(0,-a]上为减函数,在(-a,+∞)上为增函数.
(2)由(1)可知:f′(x)=![]() ,
,
①若a≥-1,则x+a≥0,即f′(x)≥0在[1,e]上恒成立,此时f(x)在[1,e]上为增函数,∴f(x)min=f(1)=-a=![]() ,∴a=-
,∴a=-![]() (舍去).
(舍去).
②若a≤-e,则x+a≤0,即f′(x)≤0在[1,e]上恒成立,
此时f(x)在[1,e]上为减函数,∴f(x)min=f(e)=1-![]() =
=![]() ,∴a=-
,∴a=-![]() (舍去).
(舍去).
③若-e<a<-1,令f′(x)=0,得x=-a,当1<x<-a时,f′(x)<0,
∴f(x)在(1,-a)上为减函数;当-a<x<e时,f′(x)>0,
∴f(x)在(-a,e)上为增函数,∴f(x)min=f(-a)=ln(-a)+1=![]() a=-
a=-![]() .
.
综上可知:a=-![]() .
.


 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】已知函数g(x)=Acos(ωx+φ)+B的部分图象如图所示,将函数g(x)的图象保持纵坐标不变,横坐标向右平移![]() 个单位长度后得到函数f(x)的图象.求:
个单位长度后得到函数f(x)的图象.求:
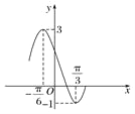
(1)函数f(x)在![]() 上的值域;
上的值域;
(2)使f(x)≥2成立的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点F与抛物线
的右焦点F与抛物线![]() 焦点重合,且椭圆的离心率为
焦点重合,且椭圆的离心率为![]() ,过
,过![]() 轴正半轴一点
轴正半轴一点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点.
两点.
(1)求椭圆的标准方程;
(2)是否存在实数![]() 使以线段
使以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,若存在,求出实数
,若存在,求出实数![]() 的值;若不存在说明理由.
的值;若不存在说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
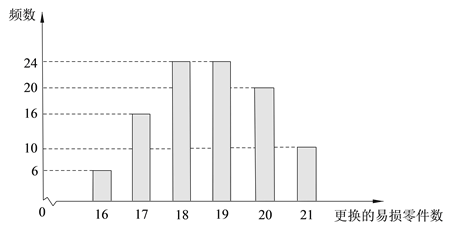
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元), ![]() 表示购机的同时购买的易损零件数.
表示购机的同时购买的易损零件数.
(Ⅰ)若![]() =19,求y与x的函数解析式;
=19,求y与x的函数解析式;
(Ⅱ)若要求“需更换的易损零件数不大于![]() ”的频率不小于0.5,求
”的频率不小于0.5,求![]() 的最小值;
的最小值;
(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2015年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| a |
|
第3组 |
| 30 | b |
第4组 |
| 20 |
|
第5组 |
| 10 |
|
合计 | 100 |
| |
![]() Ⅰ
Ⅰ![]() 求出频率分布表中a,b的值,再在答题纸上完成频率分布直方图;
求出频率分布表中a,b的值,再在答题纸上完成频率分布直方图;
![]() Ⅱ
Ⅱ![]() 根据样本频率分布直方图估计样本成绩的中位数;
根据样本频率分布直方图估计样本成绩的中位数;
![]() Ⅲ
Ⅲ![]() 高校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,再从6名学生中随机抽取2名学生由A考官进行面试,求第4组至少有一名学生被考官A面试的概率.
高校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,再从6名学生中随机抽取2名学生由A考官进行面试,求第4组至少有一名学生被考官A面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在城市旧城改造中,某小区为了升级居住环境,拟在小区的闲置地中规划一个面积为![]() 的矩形区域(如图所示),按规划要求:在矩形内的四周安排
的矩形区域(如图所示),按规划要求:在矩形内的四周安排![]() 宽的绿化,绿化造价为200元/
宽的绿化,绿化造价为200元/![]() ,中间区域地面硬化以方便后期放置各类健身器材,硬化造价为100元/
,中间区域地面硬化以方便后期放置各类健身器材,硬化造价为100元/![]() .设矩形的长为
.设矩形的长为![]() .
.

(1)设总造价![]() (元)表示为长度
(元)表示为长度![]() 的函数;
的函数;
(2)当![]() 取何值时,总造价最低,并求出最低总造价.
取何值时,总造价最低,并求出最低总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n,x的值分别为4,2,则输出v的值为 ( )
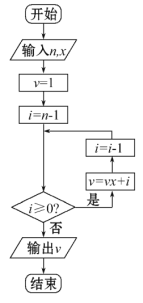
A. 9B. 18C. 25D. 50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com