
分析 (1)利用两个向量的数量积公式,三角恒等变换,化简可得f(x)的解析式.
(2)利用正弦函数的单调性,求得f(x)的单调增区间,再结合x∈[-$\frac{3}{8}$π,$\frac{3}{8}$π],得出结论.
解答 解:(1)函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=2sinxcosx 1-2cos2x=sin2x-cos2x=$\sqrt{2}$sin(2x-$\frac{π}{4}$).
(2)由f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$),可得它的最小正周期为T=$\frac{2π}{|ω|}$=π,
令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{8}$≤x≤kπ+$\frac{3π}{8}$,可得函数的增区间为[kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$],k∈Z,
再结合x∈[-$\frac{3}{8}$π,$\frac{3}{8}$π],可得函数的增区间为[-$\frac{π}{8}$,$\frac{3π}{8}$].
点评 本题主要考查两个向量的数量积公式,三角恒等变换,正弦函数的单调性,属于中档题.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
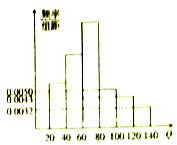 酒后违法驾驶机动车危害巨大,假设驾驶人员血液中的酒精含量为Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.如图为某市交管部门在一次夜间行动中依法查出的60名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中120≤Q<140人数包含Q≥140).
酒后违法驾驶机动车危害巨大,假设驾驶人员血液中的酒精含量为Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.如图为某市交管部门在一次夜间行动中依法查出的60名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中120≤Q<140人数包含Q≥140).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 由实数运算“(ab)t=a(bt)”类比到“($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$)” | |
| B. | 由实数运算“(ab)t=at+bt”类比到“($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•$\overrightarrow{c}$+$\overrightarrow{b}$•$\overrightarrow{c}$” | |
| C. | 由实数运算“|ab|=|a||b|”类比到“|$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|” | |
| D. | 由实数运算“$\frac{ac}{bc}$=$\frac{a}{b}$”类比到“$\frac{\overrightarrow{a}•\overrightarrow{c}}{\overrightarrow{b}•\overrightarrow{c}}$=$\frac{\overrightarrow{a}}{\overrightarrow{b}}$” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com