
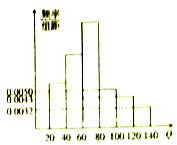
 �ƺ�Υ����ʻ������Σ�������ʻ��ԱѪҺ�еľƾ�����ΪQ�����Ѫ�ƺ�������λ�Ǻ���/100����������20��Q��80ʱ��Ϊ�ƺ�ݳ�����Q��80ʱ��Ϊ���Ƽݳ�����ͼΪij�н��ܲ�����һ��ҹ���ж������������60�����ƺ�Υ����ʻ�������߳�Ѫ��������Ƶ�ʷֲ�ֱ��ͼ������120��Q��140��������Q��140����
�ƺ�Υ����ʻ������Σ�������ʻ��ԱѪҺ�еľƾ�����ΪQ�����Ѫ�ƺ�������λ�Ǻ���/100����������20��Q��80ʱ��Ϊ�ƺ�ݳ�����Q��80ʱ��Ϊ���Ƽݳ�����ͼΪij�н��ܲ�����һ��ҹ���ж������������60�����ƺ�Υ����ʻ�������߳�Ѫ��������Ƶ�ʷֲ�ֱ��ͼ������120��Q��140��������Q��140�������� ��I������Ƶ�ʷֲ���ֱ��ͼ�����ʼ��ɵó���
��II����֪���÷ֲ������ȡ8���к������Ƽݳ���Ϊ2�ˣ�X�����п���ȡֵΪ0��1��2������P��X=k��=$\frac{{∁}_{6}^{3-k}{∁}_{2}^{k}}{{∁}_{8}^{3}}$��k=0��1��2�������ɵó���
��� �⣺��I����0.0032+0.0043+0.0050����20=0.25��0.25��60=15��
�����Ƽ�ʻ������Ϊ15���ˣ���
�� II����֪���÷ֲ������ȡ8���к������Ƽݳ���Ϊ2�ˣ�
��X�����п���ȡֵΪ0��1��2��
����P��X=k��=$\frac{{∁}_{6}^{3-k}{∁}_{2}^{k}}{{∁}_{8}^{3}}$��k=0��1��2�����ɵã�P��X=0��=$\frac{5}{14}$��P��X=1��=$\frac{15}{28}$��P��X=2��=$\frac{3}{28}$��
X�ķֲ���Ϊ
| X | 0 | 1 | 2 |
| P | $\frac{5}{14}$ | $\frac{15}{28}$ | $\frac{3}{28}$ |
���� ���⿼����Ƶ�ʷֲ���ֱ��ͼ�����ʡ��ֲ�����������ηֲ��м�����ѧ������������������������������������е��⣮


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1-i | B�� | 1+i | C�� | -1+i | D�� | -1-i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{10}}{4}$ | B�� | $\frac{10+\sqrt{10}}{5}$ | C�� | $\frac{10-\sqrt{10}}{5}$ | D�� | $\frac{10+2\sqrt{10}}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 9 | C�� | 10 | D�� | 11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com