
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
分析 求出f′(x)>0,得到函数f(x)在(-1,0)内有唯一零点,从而[f(x+3)]2015在(-4,-3)上有唯一零点;求了g′(x)=-f′(x)<0,得到g(x)在(1,2)上有唯一零点,从而[g(x-4)]2016在(5,6)上有唯一零点.由此能求出(b-a)min.
解答 解:∵f(x)=1+x-$\frac{x^2}{2}$+$\frac{x^3}{3}$-$\frac{x^4}{4}$+…+$\frac{{{x^{2015}}}}{2015}$,
∴f′(x)=(1-x)+(x2-x3)+…+x2014
=(1-x)(1+x2+x4+…+x2012)+x2014
当x=-1时,f′(x)=2×1007+1=2015>0,
当x≠-1时,f′(x)=(1-x)(1+x2+x4+…+x2012)+x2014
=(1-x)•$\frac{1-({x}^{2})^{1007}}{1-{x}^{2}}$+x2014
=$\frac{1+{x}^{2015}}{1+x}$>0,
∴f(x)=1+x-$\frac{x^2}{2}$+$\frac{x^3}{3}$-$\frac{x^4}{4}$+…+$\frac{{{x^{2015}}}}{2015}$在R上单调递增,
∴f(0)=1>0,f(-1)=1-1-$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$-…-$\frac{1}{2015}$<0,
∴函数f(x)在(-1,0)内有唯一零点,
由-1<x+3<0得:-4<x<-3,
∴f(x+3)在(-4,-3)上有唯一零点.
∴[f(x+3)]2015在(-4,-3)上有唯一零点,
∵g(x)=1-x+$\frac{x^2}{2}$-$\frac{x^3}{3}$+$\frac{x^4}{4}$-…-$\frac{{{x^{2015}}}}{2015}$,
∴g′(x)=(-1+x)+(-x2+x3)+…-x2015
=-[(1-x)+(x2-x3)+…+x2015]
=-f′(x)<0,
∴g(x)在R上单调递减,
又g(1)=1-1$+\frac{1}{2}-\frac{1}{3}+…-\frac{1}{2015}$>0,
g(2)=$1-2+\frac{{2}^{2}}{2}-\frac{{2}^{3}}{2}+…+\frac{{2}^{2014}}{2014}-\frac{{2}^{2015}}{2015}$<0,
当n≥2时,$\frac{{2}^{n}}{n}-\frac{{2}^{n+1}}{n+1}$=$\frac{{2}^{n}(1-n)}{n(n+1)}$<0,
∴g(2)<0.
∴g(x)在(1,2)上有唯一零点,
由1<x-4<2得:5<x<6,
∴g(x-4)在(5,6)上有唯一零点.
∴[g(x-4)]2016在(5,6)上有唯一零点.
∵F(x)=[f(x+3)]2015•[g(x-4)]2016,
∴F(x)的零点即为[f(x+3)]2015和[g(x-4)]2016的零点.
∴F(x)的零点区间为(-4,-3)∪(5,6).
又b,a∈Z,
∴(b-a)min=6-(-4)=10.
故选:C.
点评 本题考查两数差的最小值的求法,是中档题,解题时要认真审题,注意函数、零点、导数等知识点的综合运用.


科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,2) | C. | (3,1) | D. | (4,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 12 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
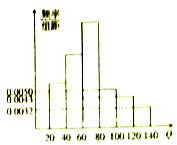 酒后违法驾驶机动车危害巨大,假设驾驶人员血液中的酒精含量为Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.如图为某市交管部门在一次夜间行动中依法查出的60名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中120≤Q<140人数包含Q≥140).
酒后违法驾驶机动车危害巨大,假设驾驶人员血液中的酒精含量为Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.如图为某市交管部门在一次夜间行动中依法查出的60名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中120≤Q<140人数包含Q≥140).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一定单调递增 | B. | 一定没有单调减区间 | ||
| C. | 可能没有单调增区间 | D. | 一定没有单调增区间 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com