考点:利用导数研究函数的单调性
专题:证明题,导数的综合应用
分析:(1)求出函数f(x)的导函数f′(x),解出f′(x)>0和f′(x)<0,从而求出函数f(x)的单调区间;
(2)构造新的函数,判断函数的单调性求出函数的最值,从而证明不等式.
解答:
解:(1)当a=0时,f(x)=e
x-2x-1(x∈R),
∵f′(x)=e
x-2,且f′(x)的零点为x=ln2,
∴当x∈(-∞,ln2)时,f′(x)<0;当x∈(ln2,+∞)时,f′(x)>0
即(-∞,ln2)是f(x)的单调减区间,(ln2,+∞)是f(x)的单调增区间.
(2)由f(x)=e
x-ax
2-2x-1(x∈R)得,f′(x)=e
x-2ax-2,
记g(x)=e
x-2ax-2(x∈R),
∵a<0,∴g′(x)=e
x-2a>0,即f′(x)=g(x)是R上的单调递增函数,
又f′(0)=-1<0,f′(1)=e-2a-2>0,
故R上存在唯一的x
0∈(0,1),使得f′(x
0)=0,且当x<x
0时,f′(x)<0;当x>x
0时,
f′(x)>0,即f(x)在(-∞,x
0)上单调递减,在(x
0,+∞)上单调递增,
则f(x)
min=f(x
0)=ex
0-ax
0-1,
再由f′(x
0)=0得ex
0=2ax
0+2,将其代入前式可得,
f(x)
min=
-ax02+2(a-1)x0+1,
又令h(x
0)=
-ax02+2(a-1)x0+1=-a
(x0-)2++1,
由于-a>0,对称轴
x=>1,而x
0∈(0,1),
∴h(x
0)>h(1)=a-1,
又
(a-1)-=->0,
∴h(x
0)>
,
故对任意实数a<0,都在f(x)>
.
点评:本题是一道导数的综合题,考查了,利用导数求函数的单调区间,等价转化思想,不等式的证明.难度中等.



 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案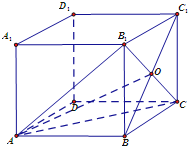 如图,在正方体ABCD-A1B1C1D1中,O是BC1与B1C的交点.
如图,在正方体ABCD-A1B1C1D1中,O是BC1与B1C的交点.