
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{17\sqrt{17}}{6}π$ | B. | 17π | C. | $\frac{17π}{2}$ | D. | $\frac{17π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | -$\frac{1}{12}$ | C. | -$\frac{1}{6}$ | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(文)试卷(解析版) 题型:解答题
已知函数 .
.
(1)当函数 在点
在点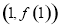 处的切线方程为
处的切线方程为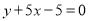 ,求函数
,求函数 的解析式;
的解析式;
(2)在(1)的条件下,若 是函数
是函数 的零点,且
的零点,且 ,求
,求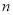 的值;
的值;
(3)当 时,函数
时,函数 有两个零点
有两个零点 ,且
,且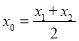 ,求证:
,求证: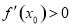 .
.
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(理)试卷(解析版) 题型:解答题
公园里有一扇形湖面,管理部门打算在湖中建一三角形观景平台,希望面积与周长都最大.如图所示扇形 ,圆心角
,圆心角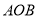 的大小等于
的大小等于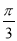 ,半径为
,半径为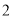 百米,在半径
百米,在半径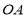 上取一点
上取一点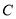 ,过点
,过点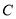 作平行于
作平行于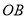 的直线交弧
的直线交弧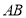 于点
于点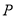 .设
.设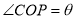 .
.
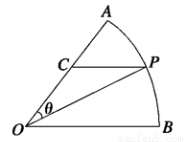
(1)求△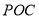 面积
面积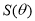 的函数表达式.
的函数表达式.
(2)求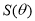 的最大值及此时
的最大值及此时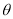 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com