
分析 (1)通过讨论m的范围,结合二次函数的性质求出m的范围即可;
(2)根问题转化为$\left\{\begin{array}{l}{{-x}^{2}+2x-1<0}\\{{x}^{2}-2x-1<0}\end{array}\right.$,解不等式组即可.
解答 解:(1)m=0时,-1<0恒成立,
m≠0时,$\left\{\begin{array}{l}{m<0}\\{△={4m}^{2}+4m<0}\end{array}\right.$,解得:-1<m<0,
综上,m的范围是(-1,0];
(2)设f(m)=(x2-2x)m-1,
由题意得$\left\{\begin{array}{l}{f(-1)<0}\\{f(1)<0}\end{array}\right.$即$\left\{\begin{array}{l}{{-x}^{2}+2x-1<0}\\{{x}^{2}-2x-1<0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x≠1}\\{1-\sqrt{2}<x<1+\sqrt{2}}\end{array}\right.$,
∴1-$\sqrt{2}$<x<1或1<x<1+$\sqrt{2}$,
故x的范围是(1-$\sqrt{2}$,1)∪(1,1+$\sqrt{2}$).
点评 本题考查了二次函数的性质,考查绝对值问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
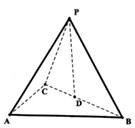 如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.
如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{2}{3},1)$ | B. | $[\frac{1}{3},1)$ | C. | $[\frac{1}{3},1)∪(1,3]$ | D. | (1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{7}}}{3}$ | B. | 3 | C. | $\frac{{\sqrt{11}}}{3}$ | D. | $\frac{{\sqrt{17}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或4 | B. | 1或4 | C. | 1或2 | D. | -6或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
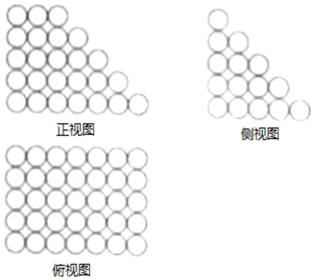 北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积.设隙积共n层,上底由长为a个物体,宽为b个物体组成,以下各层的长、宽依次各增加一个物体,最下层成为长为c个物体,宽为d个物体组成,沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}[{({2b+d})a+({b+2d})c}]+\frac{n}{6}({c-a})$.已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为85.
北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积.设隙积共n层,上底由长为a个物体,宽为b个物体组成,以下各层的长、宽依次各增加一个物体,最下层成为长为c个物体,宽为d个物体组成,沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}[{({2b+d})a+({b+2d})c}]+\frac{n}{6}({c-a})$.已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为85.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com