
分析 (1)根据直线参数方程的几何意义得出直线l的参数方程,根据极坐标与直角坐标的对应关系得出曲线C的直角坐标方程;
(2)把参数方程代入曲线C的直角坐标方程,根据参数的几何意义和根与系数的关系得出|AB|,同理得出|MN|,代入面积公式得出面积根与α的函数,根据三角函数的性质得出面积的最小值.
解答 解:(1)直线l的参数方程为$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$(t是参数).
∵ρsin2θ-4cosθ=0,∴ρ2sin2θ-4ρcosθ=0,
∴曲线C的直角坐标方程为y2-4x=0,即y2=4x.
(2)把直线l的参数方程代入y2=4x得t2sin2α-4tcosα-4=0,
设A,B对应的参数分别为t1,t2,则t1+t2=$\frac{4cosα}{si{n}^{2}α}$,t1t2=-$\frac{4}{si{n}^{2}α}$.
∴|AB|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{\frac{16co{s}^{2}α}{si{n}^{4}α}+\frac{16}{si{n}^{2}α}}$=$\frac{4}{si{n}^{2}α}$.
∵直线l′⊥l,故直线l′的倾斜角为|$α±\frac{π}{2}$|,
把α换成|$α±\frac{π}{2}$|得出|MN|=$\frac{4}{co{s}^{2}α}$.
∴四边形AMBN的面积S=$\frac{1}{2}$|AB|•|MN|=$\frac{8}{si{n}^{2}αco{s}^{2}β}$=$\frac{32}{si{n}^{2}2α}$.
∴当sin22α=1即α=45°或135°时,四边形AMBN的面积S取得最小值32.
点评 本题考查了参数方程,极坐标方程与直角坐标方程的转化,参数的几何意义,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (a-1)(b-1)<0 | B. | (a-1)(b-a)>0 | C. | (b-1)(b-a)<0 | D. | (a-1)(a-b)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” | |
| B. | 命题“?x0∈R,${x}_{0}^{2}$-x0>0”的否定是:“?x∈R,x2-x≤0” | |
| C. | 命题“p或q”为真命题,则命题p和命题q均为真命题 | |
| D. | “x>3”是“x>2”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x1,x2∈R且x1<x2,$x_1^3≥x_2^3$ | B. | ?x1,x2∈R且x1≥x2,$x_1^3≥x_2^3$ | ||
| C. | ?x1,x2∈R且x1<x2,$x_1^3≥x_2^3$ | D. | ?x1,x2∈R且x1≥x2,$x_1^3≥x_2^3$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
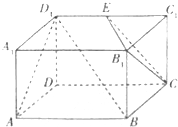 已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.
已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com