
分析 (1)由题意,根据椭圆的定义及性质求其方程;
(2)设M(x1,y1),N(x2,y2),由直线l:y=kx+t与圆(x-1)2+y2=1相切,找出k与t的关系,消去k.
再利用椭圆上一点C满足$\overrightarrow{OM}+\overrightarrow{ON}=λ\overrightarrow{OC}$,建立关系,求实数λ的取值范围.
解答 解:(1)由题意,过焦点作一直线交椭圆于E,F两点,线段|EF|长的最大值是2a,即2a=$4\sqrt{2}$,最小值时通经,即$\frac{2{b}^{2}}{a}=2\sqrt{2}$
联立:$\left\{\begin{array}{l}2a=4\sqrt{2},\;\;\\ \frac{{2{b^2}}}{a}=2\sqrt{2},\;\;\end{array}\right.$解得$\left\{\begin{array}{l}a=2\sqrt{2},\;\;\\ b=2,\;\;\end{array}\right.$
所求椭圆的方程为$\frac{x^2}{8}+\frac{y^2}{4}=1$.
(2)设M(x1,y1),N(x2,y2),由直线l:y=kx+t与圆(x-1)2+y2=1相切,圆心到直线的距离等于半径,所以:$\frac{|k+t|}{{\sqrt{{k^2}+1}}}=1⇒{t^2}+2kt-1=0,\;\;∴k=\frac{{1-{t^2}}}{2t}$…①.
∵y=kx+1与椭圆交于M,N两点:
联立$\left\{\begin{array}{l}y=kx+t,\;\;\\{x^2}+2{y^2}=8\end{array}\right.⇒(1+2{k^2}){x^2}+4ktx+2{t^2}-8=0$,
所以:${x_1}+{x_2}=-\frac{4kt}{{1+2{k^2}}},\;\;{x_1}{x_2}=\frac{{2{t^2}-8}}{{1+2{k^2}}}$,${y_1}+{y_2}=\frac{2t}{{1+2{k^2}}}$,
又∵$\overrightarrow{OM}+\overrightarrow{ON}=λ\overrightarrow{OC}$,
∴$C({\frac{-4kt}{{(1+2{k^2})λ}},\;\;\frac{2t}{{(1+2{k^2})λ}}})$,
将点C代入椭圆方程并化简得${λ^2}=\frac{t^2}{{1+2{k^2}}}$…②
①代入②得${λ^2}=\frac{{2{t^4}}}{{1+{t^4}}}<2$,解得$λ∈(-\sqrt{2},\;\;0)∪(0,\;\;\sqrt{2})$.
故实数λ的取值范围是:$(-\sqrt{2},0)∪(0,\sqrt{2})$.
点评 本题考查了椭圆方程的性质求椭圆方程,以及圆,椭圆与直线的关系.设而不求,利用向量坐标建立关系是本题的关键.同时考查了化简能力和计算能力.属于中档题.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:填空题
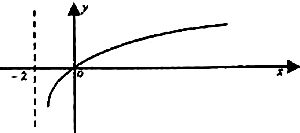 函数f(x)的定义域为(-2,+∞),部分对应值如表,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,若正数a,b满足f(2a+b)<1,则$\frac{b+2}{a+2}$的取值范围是($\frac{1}{2}$,3)
函数f(x)的定义域为(-2,+∞),部分对应值如表,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,若正数a,b满足f(2a+b)<1,则$\frac{b+2}{a+2}$的取值范围是($\frac{1}{2}$,3)| x | -1 | 0 | 4 |
| f(x) | 1 | -1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k0) | 0.10 | 0.05 | 0.01 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com