
| A. | (0,6-$\sqrt{30}$) | B. | (6-$\sqrt{30}$,2$-\sqrt{2}$) | C. | ($\frac{1}{4}$,6-$\sqrt{30}$) | D. | ($\frac{1}{4}$,2-$\sqrt{2}$) |
分析 画出函数y=f(x-1)的图象,可得y=k(x-2)+$\frac{1}{2}$与y=f(x-1)的图象最多有5个交点,即函数y=f(x-1)-$\frac{1}{2}$-k(x-2)至多有5个零点,求出函数图象交点为4个时的临界值,可得答案.
解答 解:∵y=f(x)是定义在R上的奇函数,且f(x)=$\left\{\begin{array}{l}{(x+2)^{2}-1,x<-1}\\{0,-1≤x≤0}\end{array}\right.$,
∴函数y=f(x-1)的图象如下图所示: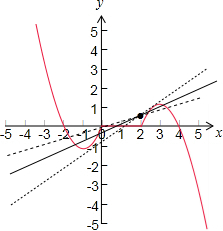
y=k(x-2)+$\frac{1}{2}$表示过(2,$\frac{1}{2}$)点斜率为k的直线,
由图可得:y=k(x-2)+$\frac{1}{2}$与y=f(x-1)的图象最多有5个交点,
即函数y=f(x-1)-$\frac{1}{2}$-k(x-2)至多有5个零点,
当k=$\frac{1}{4}$时,直线y=k(x-2)+$\frac{1}{2}$过原点,
此时y=k(x-2)+$\frac{1}{2}$与y=f(x-1)的图象有4交点,即函数y=f(x-1)-$\frac{1}{2}$-k(x-2)有4个零点;
当k=6-$\sqrt{30}$时,直线y=k(x-2)+$\frac{1}{2}$与y=f(x-1)的图象抛物线部分相切,
此时y=k(x-2)+$\frac{1}{2}$与y=f(x-1)的图象有4交点,即函数y=f(x-1)-$\frac{1}{2}$-k(x-2)有4个零点;
故当函数y=f(x-1)-$\frac{1}{2}$-k(x-2)(其中k>0)的零点个数取得最大值时,
k∈($\frac{1}{4}$,6-$\sqrt{30}$),
故选:C.
点评 本题考查的知识点是分段函数的应用,函数的零点,函数的图象,数形结合思想,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
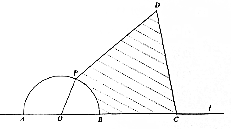 如图,直线l是湖岸线,O是l上一点,弧$\widehat{AB}$是以O为圆心的半圆形栈桥,C为湖岸线l上一观景亭,现规划在湖中建一小岛D,同时沿线段CD和DP(点P在半圆形栈桥上且不与点A,B重合)建栈桥,考虑到美观需要,设计方案为DP=DC,∠CDP=60°且圆弧栈桥BP在∠CDP的内部,已知BC=2OB=2(km),设湖岸BC与直线栈桥CD,DP是圆弧栈桥BP围成的区域(图中阴影部分)的面积为S(km2),∠BOP=θ
如图,直线l是湖岸线,O是l上一点,弧$\widehat{AB}$是以O为圆心的半圆形栈桥,C为湖岸线l上一观景亭,现规划在湖中建一小岛D,同时沿线段CD和DP(点P在半圆形栈桥上且不与点A,B重合)建栈桥,考虑到美观需要,设计方案为DP=DC,∠CDP=60°且圆弧栈桥BP在∠CDP的内部,已知BC=2OB=2(km),设湖岸BC与直线栈桥CD,DP是圆弧栈桥BP围成的区域(图中阴影部分)的面积为S(km2),∠BOP=θ查看答案和解析>>
科目:高中数学 来源: 题型:选择题
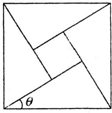 如图是由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若直角三角形中较小的内角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则tanθ的值是( )
如图是由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若直角三角形中较小的内角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则tanθ的值是( )| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
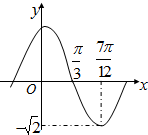 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )| A. | $f(x)=\sqrt{2}sin(\frac{1}{2}x+\frac{π}{3})$ | B. | $f(x)=\sqrt{2}sin(2x+\frac{π}{3})$ | C. | $f(x)=\sqrt{2}sin(2x+\frac{π}{6})$ | D. | $f(x)=\sqrt{2}sin(\frac{1}{2}x+\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,矩形OABC的边长OA=a,OC=1,点A,C分别在x,y正半轴上,D在AC上,$\overrightarrow{CD}$=$\frac{1}{4}$$\overrightarrow{CA}$,直线l垂直AC于D,且交直线BC于点E,交y轴于点F.
如图,矩形OABC的边长OA=a,OC=1,点A,C分别在x,y正半轴上,D在AC上,$\overrightarrow{CD}$=$\frac{1}{4}$$\overrightarrow{CA}$,直线l垂直AC于D,且交直线BC于点E,交y轴于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com