练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．若集合A={x∈Z|-2＜x＜2}，B={x|y=log2x2}，则A∩B=（　　）
    A．{-1，1}B．{-1，0，1}C．{1}D．{0，1}

    分析 化简集合A、B，根据交集的定义写出A∩B．

    解答 解：集合A={x∈Z|-2＜x＜2}={-1，0，1}，
    B={x|y=log2x2}={x|x2＞0}={x|x＜0或x＞0}，
    ∴A∩B={-1，1}．
    故选：A．

    点评 本题考查了集合的化简与运算问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．《九章算术》是我国古代数学著作，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问：积及米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积及堆放的米各为多少？”已知一斛米的体积约为1.62立方尺，由此估算出堆放的米约有（　　）
    A．21斛B．34斛C．55斛D．63斛

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．在△ABC中，角A、B、C所对的边分别为a、b、c，设向量$\overrightarrow{m}$=（a，c），$\overrightarrow{n}$=（cosC，cosA）．
    （1）若$\overrightarrow{m}$∥$\overrightarrow{n}$，a=$\sqrt{3}$c，求角A；
    （2）若$\overrightarrow{m}$•$\overrightarrow{n}$=3bsinB，cosA=$\frac{3}{5}$，求cosC的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．向量$\overrightarrow a，\overrightarrow b$满足|$\overrightarrow{a}$|=$\sqrt{2}$，|$\overrightarrow{b}$|=2，（$\overrightarrow{a}$+$\overrightarrow{b}$）⊥（2$\overrightarrow{a}$-$\overrightarrow{b}$），则向量$\overrightarrow a$与$\overrightarrow b$的夹角为（　　）
    A．45°B．60°C．90°D．120°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知集合A={x|2x-5＞0}，B={x|x2-4x+3≤0}，则A∩B=（　　）
    A．（1，$\frac{5}{2}$）B．[1，$\frac{5}{2}$）C．（$\frac{5}{2}$，3）D．（$\frac{5}{2}$，3]

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知双曲线与$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的一条渐近线被圆（x-c）2+y2=4a2截得弦长为2b（双曲线的焦距2c），则该双曲线的离心率为$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若点A（4，3），B（2，-1）在直线x+2y-a=0的两侧，则a的取值范围是（　　）
    A．（0，10）B．（-1，2）C．（0，1）D．（1，10）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

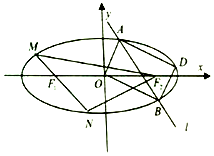    13．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），短轴长2，两焦点分别为F1，F2，过F1的直线交椭圆C于M，N两点，且△F2MN的周长为8．
    （1）求椭圆C的方程；
    （2）直线l与椭圆C相交于A，B点，点D为椭圆C上一点，四边形AOBD为矩形，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知关于x的不等式（m-1）x2+（m-1）x+2＞0
    （1）若m=0，求该不等式的解集
    （2）若该不等式的解集是R，求m的取值范围．

    查看答案和解析>>

    同步练习册答案