
| A. | $\frac{\sqrt{11}}{12}$ | B. | $\frac{\sqrt{14}}{12}$ | C. | $\frac{\sqrt{11}}{6}$ | D. | 以上都有可能 |
分析 分三种情况分别计算棱锥的体积即可.
解答 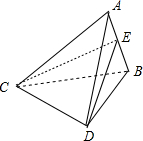 解:(1)若底边长为2,2,2,侧棱长为2,2,1;
解:(1)若底边长为2,2,2,侧棱长为2,2,1;
设AB=1,AB的中点为E,则AB⊥CE,AB⊥DE,
∴AB⊥平面CDE,
∵CE=DE=$\sqrt{{2}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{15}}{2}$,CD=2,∴cos∠CED=$\frac{C{E}^{2}+D{E}^{2}-C{D}^{2}}{2CE•DE}$=$\frac{7}{15}$,
∴sin∠CED=$\frac{4\sqrt{11}}{15}$.
∴V=$\frac{1}{3}{S}_{△CDE}•AB$=$\frac{1}{3}×\frac{1}{2}×\frac{\sqrt{15}}{2}×\frac{\sqrt{15}}{2}×\frac{4\sqrt{11}}{15}×1$=$\frac{\sqrt{11}}{6}$.
(2)若底边长为1,1,1,侧棱长为2,2,2;
设底面中心为O,则OB=$\frac{\sqrt{3}}{2}×\frac{2}{3}=\frac{\sqrt{3}}{3}$,
∴棱锥的高h=$\sqrt{{2}^{2}-(\frac{\sqrt{3}}{3})^{2}}$=$\sqrt{\frac{11}{3}}$,
∴V=$\frac{1}{3}{S}_{△BCD}•h$=$\frac{1}{3}×\frac{\sqrt{3}}{4}×\sqrt{\frac{11}{3}}$=$\frac{\sqrt{11}}{12}$.
(3)若底面边长为2,2,1,侧棱长为2,2,1,
设AB=CD=1,其余各棱长均为2,由(1)可知cos∠CED=$\frac{C{E}^{2}+D{E}^{2}-C{D}^{2}}{2CE•DE}$=$\frac{13}{15}$,
∴sin∠CED=$\frac{2\sqrt{14}}{15}$,
∴V=$\frac{1}{3}{S}_{△CDE}•AB$=$\frac{1}{3}×\frac{1}{2}×\frac{\sqrt{15}}{2}×\frac{\sqrt{15}}{2}×\frac{2\sqrt{14}}{15}×1$=$\frac{\sqrt{14}}{12}$.
故选:D.
点评 本题考查了棱锥的体积计算,属于中档题.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{3}$或2 | D. | $\frac{4}{3}$或$\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com