
(本小题满分12分)
已知函数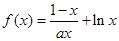
(1)若函数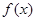 在
在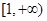 上为增函数,求正实数
上为增函数,求正实数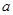 的取值范围;
的取值范围;
(2)当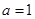 时,求
时,求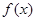 在
在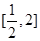 上的最大值和最小值;
上的最大值和最小值;
(3) 当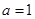 时,求证:对大于1的任意正整数
时,求证:对大于1的任意正整数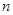 ,都有
,都有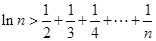 。
。
(1)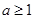 (2)最大值为
(2)最大值为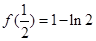 ,最小值为
,最小值为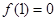 (3)
(3)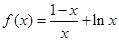 ,
,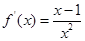
函数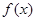 在
在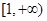 上为增函数,当
上为增函数,当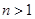 时,令
时,令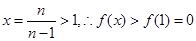
 即
即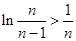 所以
所以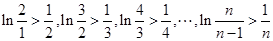
解析试题分析:(1)
科目:高中数学
来源:
题型:解答题
(本小题满分12分)
科目:高中数学
来源:
题型:解答题
(本小题满分12分)
科目:高中数学
来源:
题型:解答题
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
科目:高中数学
来源:
题型:解答题
(本小题满分14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区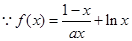 ,
,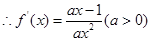
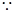 函数
函数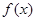 在
在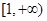 上为增函数,
上为增函数,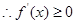 对任意的
对任意的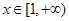 恒成立,
恒成立,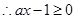 对任意的
对任意的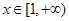 恒成立,即
恒成立,即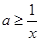 任意的
任意的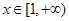 恒成立,…………2分
恒成立,…………2分
而当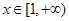 时,
时,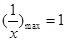 ,
,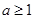 ……………………4分
……………………4分
(2)当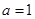 时,
时,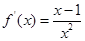
当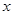 变化时,
变化时,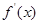 ,
,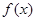 的变化情况如下表
的变化情况如下表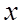
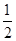
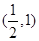
1 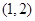
2 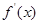
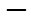
0 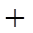
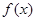
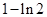
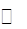
0 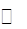


西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
萌齐小升初强化模拟训练系列答案
设函数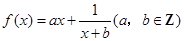 ,曲线
,曲线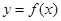 在点
在点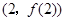 处的切线方程
处的切线方程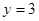 .
.
(1)求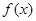 的解析式,并判断函数
的解析式,并判断函数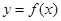 的图像是否为中心对称图形?若是,请求其对称中心;否则说明理由。
的图像是否为中心对称图形?若是,请求其对称中心;否则说明理由。
(2)证明:曲线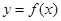 上任一点的切线与直线
上任一点的切线与直线 和直线
和直线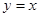 所围三角形的面积为定值,并求出此定值.
所围三角形的面积为定值,并求出此定值.
(3) 将函数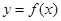 的图象向左平移一个单位后与抛物线
的图象向左平移一个单位后与抛物线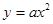 (
(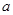 为非0常数)的图象有几个交点?(说明理由)
为非0常数)的图象有几个交点?(说明理由)
设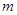 是实数,
是实数,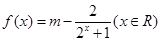 ,
,
(1)若函数 为奇函数,求
为奇函数,求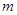 的值;
的值;
(2)试用定义证明:对于任意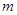 ,
, 在
在 上为单调递增函数;
上为单调递增函数;
(3)若函数 为奇函数,且不等式
为奇函数,且不等式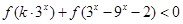 对任意
对任意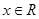 恒成立,求实数
恒成立,求实数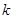 的取值范围。
的取值范围。
我们把定义在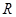 上,且满足
上,且满足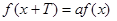 (其中常数
(其中常数 满足
满足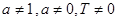 )的函数叫做似周期函数.
)的函数叫做似周期函数.
(1)若某个似周期函数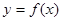 满足
满足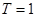 且图像关于直线
且图像关于直线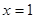 对称.求证:函数
对称.求证:函数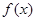 是偶函数;
是偶函数;
(2)当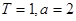 时,某个似周期函数在
时,某个似周期函数在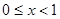 时的解析式为
时的解析式为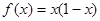 ,求函数
,求函数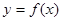 ,
,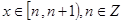 的解析式;
的解析式;
(3)对于确定的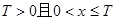 时,
时,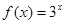 ,试研究似周期函数函数
,试研究似周期函数函数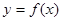 在区间
在区间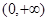 上是否可能是单调函数?若可能,求出
上是否可能是单调函数?若可能,求出 的取值范围;若不可能,请说明理由.
的取值范围;若不可能,请说明理由.
设函数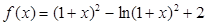 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)若不等式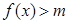 在
在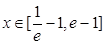 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(3)若对任意的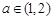 ,总存在
,总存在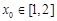 ,使不等式
,使不等式 成立,求实数m的取值范围.
成立,求实数m的取值范围.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号