练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝log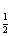 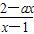(a是常数且a<2)．

    (1)求f(x)的定义域；

    (2)若f(x)在区间(2,4)上是增函数，求a的取值范围．


    　(1)∵>0，∴(ax－2)(x－1)<0，

    ①当a<0时，函数的定义域为∪(1，＋∞)；

    ②当a＝0时，函数的定义域为(1，＋∞)；

    ③当0<a<2时，函数的定义域为.

    (2)∵f(x)在(2,4)上是增函数，

    ∴只要使在(2,4)上是减函数且恒为正即可．

    令g(x)＝，

    即当x∈(2,4)时g′(x)≤0恒成立且g(4)≥0.

    解法一：g′(x)＝

    ∴当a－2<0，即a<2时，g′(x)≤0.

    g(4)≥0，即1－2a≥0，∴a≤，∴a∈

    解法二：∵g(x)＝

    ∴要使g(x)＝－a＋在(2,4)上是减函数，只需2－a>0，∴a<2，

    以下步骤同解法一．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知二次函数f(x)满足f(2)＝－1，f(－1)＝－1，且f(x)的最大值是8，试确定此二次函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)的定义域为A，若x1，x2∈A且f(x1)＝f(x2)时总有x1＝x2，则称f(x)为单函数．例如，函数f(x)＝2x＋1(x∈R)是单函数．给出下列命题：

    ①函数f(x)＝x2(x∈R)是单函数；

    ②指数函数f(x)＝2x(x∈R)是单函数；

    ③若f(x)为单函数，x1，x2∈A且x1≠x2，则f(x1)≠f(x2)；

    ④在定义域上具有单调性的函数一定是单函数．

    其中真命题是________(写出所有真命题的编号)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    方程log3(x2－10)＝1＋log3x的解是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)的定义域为A，若其值域也为A，则称区间A为f(x)的保值区间．若g(x)＝x＋m＋lnx的保值区间是[e，＋∞)，则m的值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a＝0.64.2，b＝70.6，c＝log0.67，则a，b，c的大小关系是(　　)

    A．c<b<a                                                      B．c<a<b

    C．a<c<b                                                      D．a<b<c

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)为偶函数且满足关系f(2＋x)＝f(2－x)，当－2≤x≤0时，f(x)＝2x.若n∈N＋，an＝f(n)，则a2 015等于(　　)

    A．2 013                                                       B．2

    C.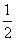                                                             D．－2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝log2x的图像大致是(　　)

    A　　　　B　　　　C　　　　D

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝(m－1)x2＋(m2－1)x＋1是偶函数，则在区间(－∞，0]上 f(x)(　　)

    A．可能是增函数，也可能是常数函数

    B．是增函数

    C．是常数函数

    D．是减函数

    查看答案和解析>>

    同步练习册答案