
| A. | 数据5,4,4,3,5,2的众数是4 | |
| B. | 若随机变量X~N(3,1)则P(X<4)=p,则(2<X<4)=1-2p | |
| C. | 数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半 | |
| D. | 频率分布直方图中各小长方形的面积等于相应各组的频数 |
分析 A,众数是4和5;
B,随机变量X~N(3,1),则正太分布曲线关于x=3对称,当P(X<4)=p时,则(2<X<4)=2p-1;
C,数据2,3,4,5分别是数据4,6,8,10的2倍,根据公式D(ax+b)=a2DX,可判定;
D,频率分布直方图中各小长方形的面积等于相应各组的频率.
解答 解:对于A,众数是4和5,故错;
对于B,随机变量X~N(3,1),则正态分布曲线关于x=3对称,当P(X<4)=p时,则(2<X<4)=2p-1,故错;
对于C,∵数据2,3,4,5分别是数据4,6,8,10的2倍,根据公式D(ax+b)=a2DX,可判定该命题正确;
对于D,频率分布直方图中各小长方形的面积等于相应各组的频率,故错;
故选:C
点评 本题考查了命题真假的判定,涉及到了统计的知识,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
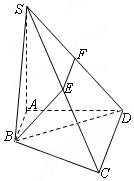 如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.
如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<7} | B. | {x|1≤x≤6} | C. | {1,2,3,4,5,6} | D. | {7,8,9} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:6$\sqrt{2}$:4 | B. | $\sqrt{2}$:12:16 | C. | $\frac{\sqrt{2}}{12}$:1:$\sqrt{2}$ | D. | $\sqrt{2}$:6:4$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com