
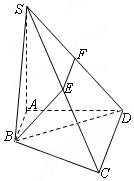
 如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.
如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.分析 (1)通过证明EF∥AB,然后证明EF∥平面SAB;
(2)连接AF,证明AF⊥SD,AF⊥EF,推出AF⊥平面SCD,然后证明BE⊥平面SCD;
(3)通过二面角B-SD-C的平面角就是90°减去B-SD-A,然后最后求解即可.
解答 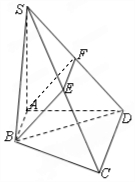 证明:(1)因为四边形ABCD是梯形,AB∥CD,E、F分别是SC、SD的中点,可得EF$\stackrel{∥}{=}$$\frac{1}{2}$CD,
证明:(1)因为四边形ABCD是梯形,AB∥CD,E、F分别是SC、SD的中点,可得EF$\stackrel{∥}{=}$$\frac{1}{2}$CD,
所以EF$\stackrel{∥}{=}$AB,AB?平面SAB,∴EF∥平面SAB;
(2)连接AF,由(1)可得EF$\stackrel{∥}{=}$AB,∴ABEF是平行四边形,AB⊥AD,F分别是SD的中点,SA=AD.∴AF⊥SD,AB⊥AD,SA⊥平面ABCD,可得AB⊥平面SAD,∴AB⊥AF,∴AF⊥EF,∴AF⊥平面SCD,BE∥AF,∴BE⊥平面SCD;
(3)由(2)可得:EF⊥平面SAD,所以二面角B-SD-C的平面角就是90°减去B-SD-A,sin∠BFA=$\frac{AB}{BF}$,二面角B-SD-C的平面角为α,
SA=AD=2CD=4AB=4.
AB=2,AF=2$\sqrt{2}$,BF=$\sqrt{4+8}$=3$\sqrt{2}$
cosα=cos(90°-∠BFA)=sin∠BFA=$\frac{AB}{BF}$=$\frac{2}{3\sqrt{2}}$=$\frac{\sqrt{2}}{3}$.
点评 本题考查直线与平面平行,二面角的平面角的求法,考查空间想象能力以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | sinα>0 | B. | cosα>0 | C. | sin2α<0 | D. | cos2α<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
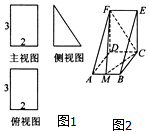 一个多面体的直观图和三视图如图所示,M是AB的 中点,一只蜜蜂在该几何体内自由飞舞,则它飞入几 何体F-AMCD内的概率为( )
一个多面体的直观图和三视图如图所示,M是AB的 中点,一只蜜蜂在该几何体内自由飞舞,则它飞入几 何体F-AMCD内的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-1,2) | C. | (-∞,0) | D. | (-∞,-2)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
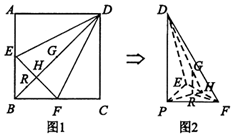 如图1,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF交于点H,G为BD中点,点R在线段BH上,且$\frac{BR}{RH}$=λ(λ>0).现将△AED,△CFD,△DEF分别沿DE,DF,EF折起,使点A,C重合于点B(该点记为P),如图2所示.
如图1,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF交于点H,G为BD中点,点R在线段BH上,且$\frac{BR}{RH}$=λ(λ>0).现将△AED,△CFD,△DEF分别沿DE,DF,EF折起,使点A,C重合于点B(该点记为P),如图2所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 数据5,4,4,3,5,2的众数是4 | |
| B. | 若随机变量X~N(3,1)则P(X<4)=p,则(2<X<4)=1-2p | |
| C. | 数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半 | |
| D. | 频率分布直方图中各小长方形的面积等于相应各组的频数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com