
分析 由已知,三棱锥P-ABC的四个顶点均在半径为3的球面上,且PA,PB,PC两两垂直,球直径等于以PA,PB,PC为棱的长方体的对角线,由基本不等式易得到三棱锥P-ABC的侧面积的最大值.
解答 解:∵PA,PB,PC两两垂直,
又∵三棱锥P-ABC的四个顶点均在半径为3的球面上,
∴以PA,PB,PC为棱的长方体的对角线即为球的一条直径.
∴64=PA2+PB2+PC2,
则由基本不等式可得PA2+PB2≥2PA•PB,PA2+PC2≥2PA•PC,PB2+PC2≥2PB•PC,
即64=PA2+PB2+PC2≥PA•PB+PB•PC+PA•PC
则三棱锥P-ABC的侧面积S=$\frac{1}{2}$(PA•PB+PB•PC+PA•PC)≤32,
则三棱锥P-ABC的侧面积的最大值为32,
故答案为:32.
点评 本题考查的知识点是棱锥的侧面积,基本不等式,棱柱的外接球,其中根据已知条件,得到棱锥的外接球直径等于以PA,PB,PC为棱的长方体的对角线,是解答本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
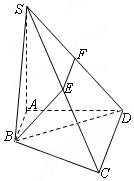 如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.
如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
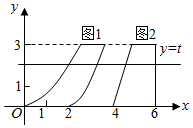 我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容 异”.“势’’即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为l的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图l和图2所截得的两线段长始终相等,则图l的面积为$\frac{9}{2}$.
我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容 异”.“势’’即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为l的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图l和图2所截得的两线段长始终相等,则图l的面积为$\frac{9}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<7} | B. | {x|1≤x≤6} | C. | {1,2,3,4,5,6} | D. | {7,8,9} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com