
分析 由题意判断出三角形有两解时,A的范围,通过正弦定理及正弦函数的性质推出x的范围即可.
解答 解:由AC=b=2,要使三角形有两解,就是要使以C为圆心,半径为2的圆与BA有两个交点,
当A=90°时,圆与AB相切;
当A=30°时交于B点,也就是只有一解,
∴30°<A<150°,且A≠90°,即 $\frac{1}{2}$<sinA<1,
由正弦定理以及asinB=bsinA.可得:a=x=$\frac{bsinA}{sinB}$=4sinA,
∵4sinA∈(2,4 ).
∴x的取值范围是(2,4 ).
故答案为:(2,4 ).
点评 此题考查了正弦定理,正弦函数的图象与性质,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:填空题
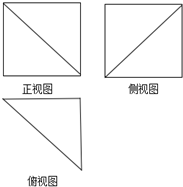 如图是某几何体的三视图,其中正视图为正方形,俯视图是腰长为2的等腰直角三角形,则该几何体的体积为$\underline{\frac{8}{3}}$;表面积为6+4$\sqrt{2}+2\sqrt{3}$.
如图是某几何体的三视图,其中正视图为正方形,俯视图是腰长为2的等腰直角三角形,则该几何体的体积为$\underline{\frac{8}{3}}$;表面积为6+4$\sqrt{2}+2\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -l | B. | 1 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α>β,则sinα>sinβ | |
| B. | 数列{an},{bn}为等比数列,则数列{an+bn}为等比数列 | |
| C. | 函数f(x),g(x)均为增函数,则函数f(x)•g(x)为增函数 | |
| D. | 在△ABC中,若a>b,则sinA>sinB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com