
分析 ①:?a=b=0∈S,满足S<T.
②:?a,b∈S,都有a-b,ab为偶数;?r∈S,n∈T,都有rn为偶数,满足S<T.
③:?r∈S,n∈T,可能rn为虚数,因此rn∉S.则S不是T的一个理想.
解答 解:①:?a,b∈S,都有a-b=0-0=0∈S且0×0=0∈S;?r=0∈S,n∈T,都有rn=0∈S.则S是T的一个理想,即S<T.
②:?a,b∈S,都有a-b,ab为偶数,因此a-b∈S且ab∈S;?r∈S,n∈T,都有rn为偶数,因此rn∈S.则S是T的一个理想,即S<T.
③:?a,b∈S,都有a-b,ab实数,因此a-b∈S且ab∈S;?r∈S,n∈T,可能rn为虚数,因此rn∉S.则S不是T的一个理想.
其中满足S<T的集合对的序号是 ①②.
故答案为:①②.
点评 本题考查了新定义、元素与集合之间的关系、分类讨论方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
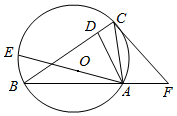 如图,AE是⊙O的直径,△ABC内接于⊙O,AB=BC,AD⊥BC,垂足为D.
如图,AE是⊙O的直径,△ABC内接于⊙O,AB=BC,AD⊥BC,垂足为D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 90° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在空间多面体ABCDE中,四边形ABCD为直角梯形,AB∥DC,AD⊥CD,△ADE是正三角形,CD=DE=2AB,CE=$\sqrt{2}$CD.
如图,在空间多面体ABCDE中,四边形ABCD为直角梯形,AB∥DC,AD⊥CD,△ADE是正三角形,CD=DE=2AB,CE=$\sqrt{2}$CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com