
| A�� | 120�� | B�� | 90�� | C�� | 60�� | D�� | 30�� |
���� ���������õ�$|\overrightarrow{a}|=1��|\overrightarrow{b}|=1$���Ӷ���������������������$\overrightarrow{a}•��\overrightarrow{a}-2\overrightarrow{b}��=2$�õ�$cos��\overrightarrow{a}��\overrightarrow{b}��=-\frac{1}{2}$�������������нǵķ�Χ���ɵó�����$\overrightarrow{a}��\overrightarrow{b}$�ļнǣ�
��� �⣺�������⣬$|\overrightarrow{a}|=|\overrightarrow{b}|=1$��
��$\overrightarrow{a}•��\overrightarrow{a}-2\overrightarrow{b}��={\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}$=$1-2cos��\overrightarrow{a}��\overrightarrow{b}��=2$��
��$cos��\overrightarrow{a}��\overrightarrow{b}��=-\frac{1}{2}$��
��$0��ܣ�\overrightarrow{a}��\overrightarrow{b}����180��$��
������$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ120�㣮
��ѡ��A��
���� ���鵥λ�����ĸ�����������������㼰���㹫ʽ���Լ������нǵķ�Χ����֪���Ǻ���ֵ��ǣ�


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10 | B�� | 15 | C�� | 35 | D�� | 75 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
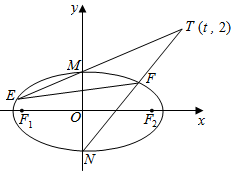 ��֪��ԲC��$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0�����϶���M�����ҽ���F1��F2����������MF1F2���Ϊ$\sqrt{3}$������ԲC��������Ϊ$\frac{{\sqrt{3}}}{2}$��
��֪��ԲC��$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0�����϶���M�����ҽ���F1��F2����������MF1F2���Ϊ$\sqrt{3}$������ԲC��������Ϊ$\frac{{\sqrt{3}}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{2}$ | B�� | -$\frac{3}{2}$ | C�� | ��$\frac{3}{2}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{2}{3}$ | B�� | -$\frac{1}{3}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 132 | B�� | 66 | C�� | 33 | D�� | 11 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com