考点:利用导数研究函数的单调性,利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)化简
,并求导数,注意定义域:(0,+∞),求出单调区间;
(Ⅱ)运用零点存在定理说明
在(1,2)内有零点,再说明f(x)在(0,+∞)上有且只有两个零点;
(Ⅲ)对g(x)化简,并求出导数,整理合并,再设出h(x)=x
2-(2+a)x+1,说明h(x)=0的两个根,有一个在(0,
)内,另一个大于e,由于h(0)=1,通过h(
)>0解出a即可.
解答:
解:(Ⅰ)设φ(x)=
=x
2-1-
(x>0),
则φ'(x)=2x+
>0,
∴φ(x)在(0,+∞)上单调递增;
(Ⅱ)∵φ(1)=-1<0,φ(2)=3-
>0,且φ(x)在(0,+∞)上单调递增,
∴φ(x)在(1,2)内有零点,
又f(x)=x
3-x-
=x•φ(x),显然x=0为f(x)的一个零点,
∴f(x)在(0,+∞)上有且只有两个零点;
(Ⅲ)g(x)=
+lnx=lnx+
,
则g'(x)=
-=
,
设h(x)=x
2-(2+a)x+1,
则h(x)=0有两个不同的根x
1,x
2,且有一根在(0,
)内,
不妨设0<x
1<
,由于x
1x
2=1,即x
2>e,
由于h(0)=1,故只需h(
)<0即可,
即
-(2+a)
•+1<0,解得a>e+
-2,
∴实数a的取值范围是(e+
-2,+∞).
点评:本题主要考查导数在函数中的综合运用:求单调区间,求极值,同时考查零点存在定理和二次方程实根的分布,是一道综合题.



 名校课堂系列答案
名校课堂系列答案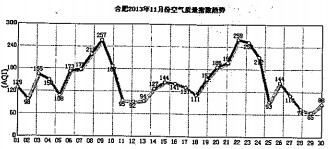 合肥市环保总站对2013年11月合肥市空气质量指数发布如图趋势图.
合肥市环保总站对2013年11月合肥市空气质量指数发布如图趋势图.