
【题目】已知![]() 是椭圆
是椭圆![]() 的两个焦点,
的两个焦点,![]() 是椭圆
是椭圆![]() 上一点,当
上一点,当![]() 时,有
时,有![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点![]() 的动直线
的动直线![]() 与椭圆交于
与椭圆交于![]() 两点,试问在
两点,试问在![]() 铀上是否存在与
铀上是否存在与![]() 不重合的定点
不重合的定点![]() ,使得
,使得![]() 恒成立?若存在,求出定点
恒成立?若存在,求出定点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)![]()
(2)存在, T(4,0)
【解析】
(1)由题意,![]() .故
.故![]() .然后设点
.然后设点![]() 坐标为
坐标为![]() ,代入椭圆方程,联立椭圆定义
,代入椭圆方程,联立椭圆定义![]() ,进一步计算可得椭圆
,进一步计算可得椭圆![]() 的标准方程;
的标准方程;
(2)假设存在与![]() 不重合的定点
不重合的定点![]() ,使得
,使得![]() 恒成立,则
恒成立,则![]() ,设出
,设出![]() 、
、![]() 、
、![]() 点坐标代入
点坐标代入![]() 计算,可得
计算,可得![]() .然后设直线
.然后设直线![]() .联立直线与椭圆方程,消去
.联立直线与椭圆方程,消去![]() 整理可得一元二次方程,根据韦达定理有
整理可得一元二次方程,根据韦达定理有![]() ,
,![]() .然后代入
.然后代入![]() 进行计算可判断是否是定值,即可得到结论.
进行计算可判断是否是定值,即可得到结论.
解:(1)由题意,![]() .故
.故![]() .
.
可设点![]() 坐标为
坐标为![]() ,则
,则
![]() ,解得
,解得![]() ,即
,即![]() .
.
![]() ,解得
,解得![]() .
.
![]() ,
,![]() .
.
![]() 椭圆
椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由题意,假设存在与![]() 不重合的定点
不重合的定点![]() ,使得
,使得![]() 恒成立,
恒成立,
设![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则
![]() ,
,![]() .
.
![]() ,
,
![]() ,即
,即![]() .
.
整理,得![]() .
.
设直线![]() .
.
联立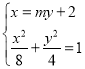 ,
,
消去![]() ,整理得
,整理得![]() .
.
![]()
![]() ,
,![]() .
.
![]()
![]() .
.
![]()
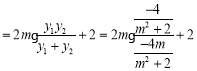
![]() .
.
![]() 存在与
存在与![]() 不重合的定点
不重合的定点![]() ,使得
,使得![]() 恒成立,且点
恒成立,且点![]() 坐标为
坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知等比数列![]() 的前n项和为
的前n项和为![]() ,且当
,且当![]() 时,
时,![]() 是
是![]() 与2m的等差中项
与2m的等差中项![]() 为实数
为实数![]() .
.
(1)求m的值及数列![]() 的通项公式;
的通项公式;
(2)令![]() ,是否存在正整数k,使得
,是否存在正整数k,使得![]() 对任意正整数n均成立?若存在,求出k的最大值;若不存在,说明理由.
对任意正整数n均成立?若存在,求出k的最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系下,已知圆O:ρ=cosθ+sinθ和直线l:![]() .
.
(1)求圆O和直线l的直角坐标方程;
(2)当θ∈(0,π)时,求直线l与圆O公共点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是AB的垂直平分线,
是AB的垂直平分线,
(1)当且仅当![]() 取何值时,直线
取何值时,直线![]() 经过抛物线的焦点F?证明你的结论;
经过抛物线的焦点F?证明你的结论;
(2)若![]() ,弦AB是否过定点,若过定点,求出该定点,若不过定点,说明理由.
,弦AB是否过定点,若过定点,求出该定点,若不过定点,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个口袋有m个白球,n个黑球(m,n![]()
![]() ,n
,n![]() 2),这些球除颜色外全部相同。现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,……,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,……,m+n).
2),这些球除颜色外全部相同。现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,……,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,……,m+n).
![]()
(1)试求编号为2的抽屉内放的是黑球的概率p;
(2)随机变量x表示最后一个取出的黑球所在抽屉编号的倒数,E(x)是x的数学期望,证明 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的发展,各种“APP”(英文单词Application的缩写,一般指手机软件)应运而生.某机构欲对A市居民手机内安装的APP的个数和用途进行调研,在使用智能手机的居民中随机抽取100人,获得了他们手机内安装APP的个数,整理得到如图所示频率分布直方图.

(Ⅰ)求a的值;
(Ⅱ)从被抽取安装APP的个数不低于50的居民中,随机抽取2人进一步调研,求这2人安装APP的个数都低于60的概率;
(Ⅲ)假设同组中的数据用该组区间的右端点值代替,以本次被抽取的居民情况为参考,试估计A市使用智能手机的居民手机内安装APP的平均个数在第几组(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在极坐标系中,O为极点,点![]() 在曲线
在曲线![]() 上,直线l过点
上,直线l过点![]() 且与
且与![]() 垂直,垂足为P.
垂直,垂足为P.
(1)当![]() 时,求
时,求![]() 及l的极坐标方程;
及l的极坐标方程;
(2)当M在C上运动且P在线段OM上时,求P点轨迹的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com