
 的函数
的函数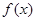 ,定义
,定义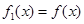 ,
,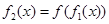 ,…,
,…,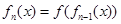 ,n=1,2,3,….满足
,n=1,2,3,….满足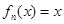 的点称为f的
的点称为f的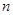 阶周期点.
阶周期点.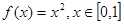 则f的
则f的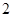 阶周期点的个数是___________;
阶周期点的个数是___________;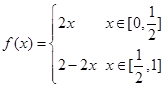 则f的
则f的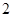 阶周期点的个数是__________ .
阶周期点的个数是__________ .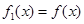 =
=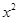 ,由
,由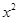 =x得,x=0,1,f的1阶周期点的个数是2;
=x得,x=0,1,f的1阶周期点的个数是2;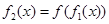 =
=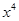 ,由
,由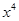 =x,得x=0,1,所以f的
=x,得x=0,1,所以f的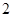 阶周期点的个数是2.
阶周期点的个数是2.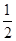 ]时,f1(x)=2x=x,解得x=0,
]时,f1(x)=2x=x,解得x=0,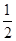 ,1]时,f1(x)=2-2x=x,解得x=
,1]时,f1(x)=2-2x=x,解得x=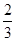 ,∴f的1阶周期点的个数是2;
,∴f的1阶周期点的个数是2;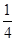 ]时,f1(x)=2x,f2(x)=4x=x,解得x=0;
]时,f1(x)=2x,f2(x)=4x=x,解得x=0;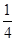 ,
,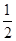 ]时,f1(x)=2x,f2(x)=2-4x=x,解得x=
]时,f1(x)=2x,f2(x)=2-4x=x,解得x=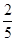 ;
;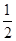 ,
,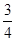 ]时,f1(x)=2-2x,f2(x)=-2+4x=x,解得x=
]时,f1(x)=2-2x,f2(x)=-2+4x=x,解得x=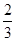 ;
;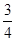 ,1]时,f1(x)=2-2x,f2(x)=4-4x=x,解得x=
,1]时,f1(x)=2-2x,f2(x)=4-4x=x,解得x=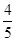 .∴f的2阶周期点的个数是22=4.
.∴f的2阶周期点的个数是22=4.

科目:高中数学 来源:不详 题型:填空题
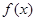 的定义域为
的定义域为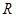 ,且满足
,且满足 为 奇函数,
为 奇函数,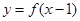 为偶函数,则下列说法中一定正确的有
为偶函数,则下列说法中一定正确的有 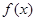 的图像关于直线
的图像关于直线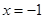 对称
对称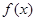 的周期为
的周期为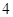
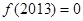
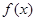 在
在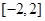 上只有一个零点
上只有一个零点查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.| 运输工具 | 运输费单价:元/(吨•千米) | 冷藏费单价:元/(吨•时) | 固定费用:元/次 |
| 汽车 | 2 | 5 | 200 |
| 火车 | 1.6 | 5 | 2280 |

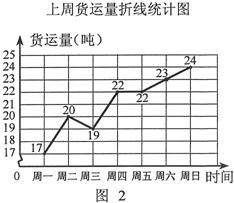
 汽(元)和
汽(元)和 火(元),分别求
火(元),分别求 汽、
汽、 火与
火与  的函数关系式(不必写出
的函数关系式(不必写出 的取值范围),及
的取值范围),及 为何值时
为何值时 汽>
汽> 火(总费用=运输费+冷藏费+固定费用)
火(总费用=运输费+冷藏费+固定费用)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com