
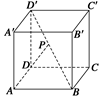
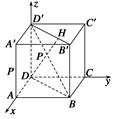
 =(1,0,0),
=(1,0,0), =(0,0,1).
=(0,0,1). ="(m,m,1)" (m>0),由已知〈
="(m,m,1)" (m>0),由已知〈 ,
, 〉=60°,
〉=60°, ·
· =|
=| ||
|| |cos〈
|cos〈 ,
,  〉,
〉, .
. ,所以
,所以 =(
=( ,
, ,1).
,1). ,
, 〉=
〉= =
= ,
, ,
, 〉=45°,
〉=45°,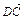 =(0,1,0).
=(0,1,0). ,
,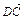 〉=
〉= =
= ,
, ,
,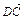 〉=60°,
〉=60°,

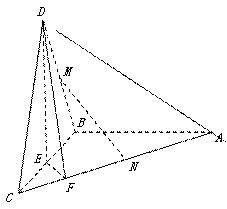
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源:不详 题型:解答题
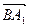 ,
,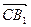 )的值;
)的值;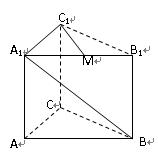
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 B
B C
C D
D 中,底面边长为2
中,底面边长为2 ,侧棱长为4,点E、F分别为棱AB、BC的中点,EF∩BD=G,求点D
,侧棱长为4,点E、F分别为棱AB、BC的中点,EF∩BD=G,求点D 到平面B
到平面B EF的距离d。
EF的距离d。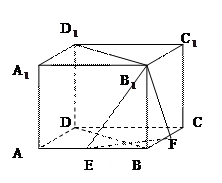
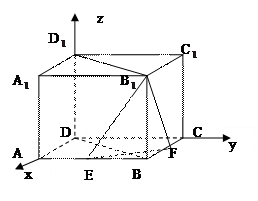
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
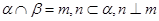 ,则
,则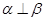 ;②若
;②若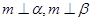 ,则
,则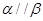 ;③若
;③若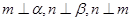 ,则
,则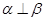 ;④若
;④若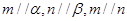 ,则
,则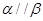 ,其中正确的命题是( )
,其中正确的命题是( )| A.①② | B.②③ | C.③④ | D.①③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com