
(本题满分12分)已知四棱锥P-ABCD,底面ABCD是 、边长为
、边长为 的菱形,又
的菱形,又 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.

(1)证明:DN//平面PMB;
(2)证明:平面PMB 平面PAD;
平面PAD;
(3)求点A到平面PMB的距离.
(1)证明见解析;(2)证明见解析;(3)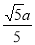
【解析】
试题分析:(1)解决立体几何的有关问题,空间想象能力是非常重要的,但新旧知识的迁移融合也很重要,在平面几何的基础上,把某些空间问题转化为平面问题来解决,有时很方便;(2)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质,证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化;(3)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键.
试题解析:(1)证明:取PB中点Q,连结MQ、NQ,
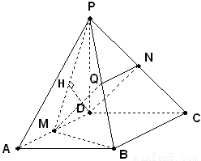
因为M、N分别是棱AD、PC中点,所以
QN//BC//MD,且QN=MD,于是DN//MQ.
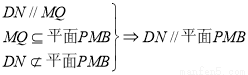 4分
4分
(2)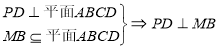
又因为底面ABCD是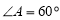 、边长为
、边长为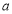 的菱形,且M为AD中点,
的菱形,且M为AD中点,
所以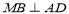 .又
.又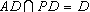 所以
所以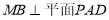 .
.
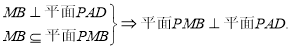 8分
8分
(3)因为M是AD中点,所以点A与D到平面PMB等距离.
过点D作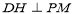 于H,由(2)平面PMB
于H,由(2)平面PMB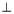 平面PAD,所以
平面PAD,所以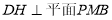 .
.
故DH是点D到平面PMB的距离.
 所以点A到平面PMB的距离为
所以点A到平面PMB的距离为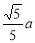 . 12分
. 12分
考点:1、直线与平面平行的判定;2、平面与平面垂直的判定;3、点到平面的距离.
考点分析: 考点1:点、线、面之间的位置关系 试题属性

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源:2014-2015学年广东省汕头市高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)某中学一名数学老师对全班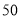 名学生某次考试成绩分男女生进行了统计(满分
名学生某次考试成绩分男女生进行了统计(满分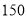 分),其中
分),其中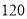 分(含
分(含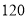 分)以上为优秀,绘制了如下的两个频率分布直方图:
分)以上为优秀,绘制了如下的两个频率分布直方图:
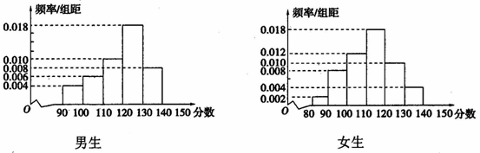
(1)根据以上两个直方图完成下面的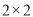 列联表:
列联表:

(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?

(3)若从成绩在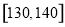 的学生中任取
的学生中任取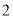 人,求取到的
人,求取到的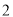 人中至少有
人中至少有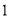 名女生的概率.
名女生的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省兰州市高三诊断考试理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-5:不等式选讲
已知函数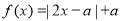 .
.
(1)若不等式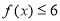 的解集为
的解集为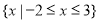 ,求实数
,求实数 的值;
的值;
(2)在(1)的条件下,若存在实数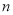 使
使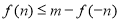 成立,求实数
成立,求实数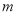 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高三第一次联考文科数学试卷(解析版) 题型:解答题
(本小题满分l0分)选修4—5:不等式选讲
已知函数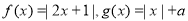
(1)当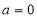 时,解不等式
时,解不等式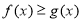 ;
;
(2)若存在 ,使得,
,使得,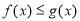 成立,求实数
成立,求实数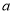 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高三第一次联考理科数学试卷(解析版) 题型:填空题
正四棱锥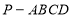 的五个顶点在同一球面上,若正四棱锥的底面边长是
的五个顶点在同一球面上,若正四棱锥的底面边长是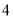 ,侧棱长为
,侧棱长为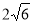 ,则此球的表面积___________.
,则此球的表面积___________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省福州市高三毕业班第六次质量检查理科数学试卷(解析版) 题型:解答题
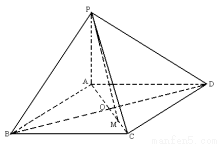
(本小题满分13分)已知四棱锥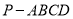 中,
中,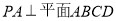 ,底面
,底面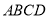 是边长为
是边长为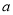 的菱形,
的菱形,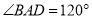 ,
,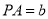 .
.
(Ⅰ)求证: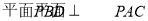 ;
;
(Ⅱ)设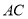 与
与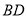 交于点
交于点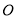 ,
,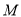 为
为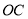 中点,若二面角
中点,若二面角 的正切值为
的正切值为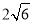 ,求
,求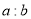 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com