已知数列{an}中，a3=8，an+1=2an
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=log2an，求数列{bn}的前n项和Sn．
科目：高中数学 来源： 题型：
为了解一片经济林的生长情况，随机测量了其中100株树木的底部周长（单位：cm）．根据所得数据画出样本的频率分布直方图（如右），那么在这100株树木中，底部周长小于110cm的株数是 _________ ．
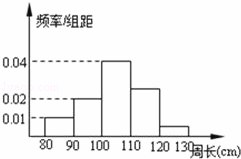
查看答案和解析>>
科目：高中数学 来源： 题型：
设等差数列{an}的前n项和Sn，若S15＞0，S16＜0，则数列{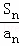
}的前15项中最大的项是（ ）
|
| A． | 第1项 | B． | 第8项 | C． | 第9项 | D． | 第15项 |
查看答案和解析>>
科目：高中数学 来源： 题型：
在平面直角坐标系中，定义d（P，Q）=|x1﹣x2|+|y1﹣y2|为两点P（x1，y1），Q（x2，y2）之间的“折线距离”，在这个定义下，给出下列命题：
①到原点的“折线距离”等于1的点的集合是一个圆；
②到原点的“折线距离”小于等于2的点构成的区域面积为8；
③到M（0，﹣2），N（0，2）两点的“折线距离”相等的点的轨迹方程是y=0；
④直线y=x+1上的点到N（0，2）的“折线距离”的最小值为1．
其中真命题有（ ）
|
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
查看答案和解析>>
科目：高中数学 来源： 题型：
已知等差数列{an}中，a3=8，a10=18，三点（a1，0）、（a2，0）、（a3，0）在圆C上，
（Ⅰ）求圆C的方程；
（Ⅱ）若直线l：mx+ny+1=0被圆C所截得的弦长为2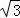
，求m2+n2的最小值；
（Ⅲ）若一条动直线与圆C交于A、B两点，且总有|OA|•|OB|=8，（点O为坐标原点），试探究直线AB是否恒与一个定圆相切，并说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
演绎推理“因为对数函数y=logax（a＞0且a≠1）是增函数，而函数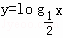
是对数函数，所以
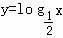是增函数”所得结论错误的原因是（ ）
|
| A． | 大前提错误 | B． | 小前提错误 |
|
| C． | 推理形式错误 | D． | 大前提和小前提都错误 |
查看答案和解析>>
科目：高中数学 来源： 题型：
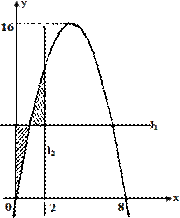已知二次函数
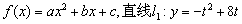(其中
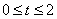,t为常数）,
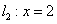的图象如图所示.
（1）根据图象求a、b、c的值；
（2）求阴影面积S关于t的函数S(t)的解析式；
（3）若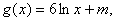
问是否存在实数m， 使得
的图象与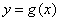
的图象有且只有三个不同的
交点？若存在，求出m的值；若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
满足
（其中i为虚数单位），则
B.
C.
D.