
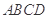 为正方形,
为正方形,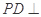 平面
平面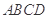 ,
,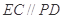 ,且
,且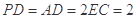
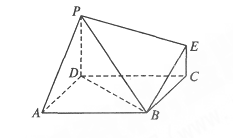
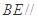 平面
平面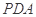 ;
; 的体积;
的体积;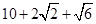 .
.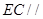 平面
平面 ,
,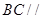 平面
平面 ,所以可得到平面
,所以可得到平面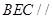 平面
平面 ,所以利用面面平行的性质得证结论;第二问,利用线面垂直得到线线垂直
,所以利用面面平行的性质得证结论;第二问,利用线面垂直得到线线垂直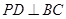 ,又因为
,又因为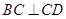 ,所以得到线面垂直,所以
,所以得到线面垂直,所以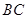 是所求锥体的高,利用梯形面积公式求底面
是所求锥体的高,利用梯形面积公式求底面 的面积,再利用体积公式求体积;第三问,利用已知的边的关系和长度,可以求出组合体中每一条边的长度,从而求出每一个面的面积,最后求和加在一起即可.
的面积,再利用体积公式求体积;第三问,利用已知的边的关系和长度,可以求出组合体中每一条边的长度,从而求出每一个面的面积,最后求和加在一起即可.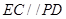 ,
,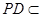 平面
平面 ,
,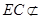 平面
平面 ,
,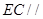 平面
平面 ,
,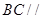 平面
平面 ,
,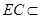 平面
平面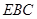 ,
,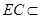 平面
平面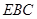 ,且
,且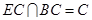 ,
,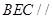 平面
平面 ,
,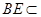 平面
平面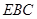 ,∴
,∴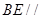 平面
平面 ,
,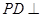 平面
平面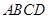 ,
,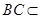 平面
平面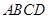 ,
,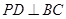 ,
,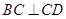 ,
,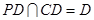
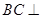 平面
平面 ,
,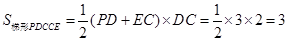 ,
,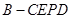 的体积
的体积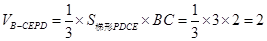 ,
,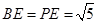 ,
,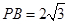 ,
, ,
,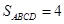 ,
,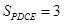 ,
,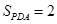 ,
, ,
,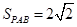 ,
,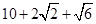 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
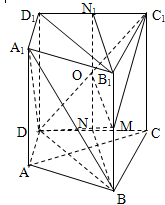
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
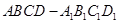 的棱长为
的棱长为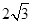 ,动点P在对角线
,动点P在对角线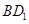 上,过点P作垂直于
上,过点P作垂直于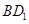 的平面
的平面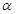 ,记这样得到的截面多边形(含三角形)的周长为y,设
,记这样得到的截面多边形(含三角形)的周长为y,设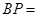 x,则当
x,则当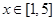 时,函数
时,函数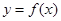 的值域为( )
的值域为( )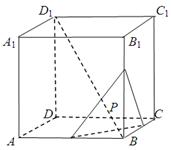
A.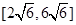 | B.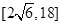 | C.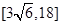 | D.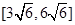 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.如果平面 ,那么平面 ,那么平面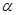 内一定存在直线平行于平面 内一定存在直线平行于平面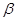 ; ; |
B.如果平面α不垂直于平面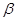 ,那么平面 ,那么平面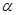 内一定不存在直线垂直于平面 内一定不存在直线垂直于平面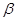 ; ; |
C.如果平面 ,平面 ,平面 , ,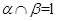 ,那么 ,那么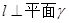 ; ; |
D.如果平面 ,那么平面 ,那么平面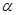 内所有直线都垂直于平面 内所有直线都垂直于平面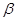 . . |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
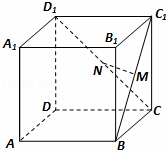
| A.MN与CC1垂直 | B.MN与AC垂直 | C.MN与BD平行 | D.MN与A1B1平行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com