
已知函数 的图像经过点
的图像经过点 .
.
(1)求 的值;
的值;
(2)在 中,
中,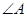 、
、 、
、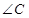 所对的边分别为
所对的边分别为 、
、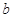 、
、 ,若
,若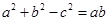 ,且
,且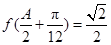 .求
.求 .
.
(1)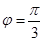 (2)sinB=
(2)sinB=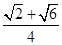
解析试题分析:
(1)f(x)的图像经过点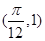 ,带入函数得到关于
,带入函数得到关于 的三角等式,再利用常见三角函数值与
的三角等式,再利用常见三角函数值与 的范围即可求出
的范围即可求出 的值.
的值.
(2)利用三角形关于C角的余弦定理与题目已知式子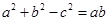 结合即可得出C角的余弦值,进而得到C角的正弦值(三角形内角的正弦值都为正数),再把
结合即可得出C角的余弦值,进而得到C角的正弦值(三角形内角的正弦值都为正数),再把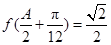 带入函数解析式即可得到A角的余弦,利用余弦与正弦的关系得到A角的正弦值,而三角形三个角和为180度,则B角的正弦利用和差角公式即可用A,C两个角的正余弦值来表示,进而得到B角的余弦值.
带入函数解析式即可得到A角的余弦,利用余弦与正弦的关系得到A角的正弦值,而三角形三个角和为180度,则B角的正弦利用和差角公式即可用A,C两个角的正余弦值来表示,进而得到B角的余弦值.
试题解析:
(1)由题意可得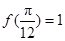 ,即
,即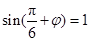 . 2分
. 2分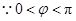 ,
,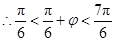 ,
,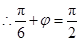 ,
,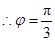 . 5分
. 5分
(2)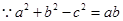 ,
,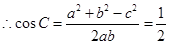 , 7分
, 7分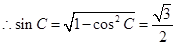 . 8分
. 8分
由(1)知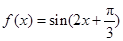 ,
,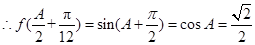 .
.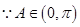 ,
, 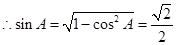 , 10分
, 10分
又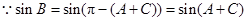 ,
,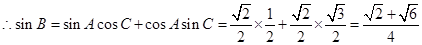 . 12分
. 12分
考点:三角函数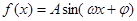 的图象与性质,三角恒等变换 余弦定理
的图象与性质,三角恒等变换 余弦定理


科目:高中数学 来源: 题型:解答题
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;
(3)是否存在v,使得小艇以v海里/时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定v的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在锐角△ABC中,角A,B,C所对的边分别为a,b,c,向量m=(1,cosB),n=(sinB,- ),且m⊥n.
),且m⊥n.
(1)求角B的大小.
(2)若△ABC的面积为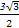 ,a=2,求b的值.
,a=2,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com