练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．设集合A={x|x2-3x+2≤0}，B={（x，y）|x∈A，y∈A}，则A∩B=（　　）
    A．AB．BC．A∪BD．∅

    分析 求解一元二次不等式化简集合A，可知A是数集，集合B是点集，则A∩B是空集．

    解答 解：集合A={x|x2-3x+2≤0}={x|1≤x≤2}，
    B={（x，y）|x∈A，y∈A}={（x，y）|$\left\{\begin{array}{l}{1≤x≤2}\\{1≤y≤2}\end{array}\right.$}，
    ∵A为数集，B为点集，
    ∴A∩B=∅．
    故选：D．

    点评 本题考查了集合的定义与运算问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．直线l与曲线y=ex相切于点A（0，1），直线l的方程是x-y+1=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．在平面直角坐标系xoy中，已知圆C的参数方程为$\left\{{\begin{array}{l}{x=1+2cosθ}\\{y=2sinθ}\end{array}}\right.$（θ为参数），直线l的参数方程为$\left\{{\begin{array}{l}{x=5-2t}\\{y=3-t}\end{array}}\right.$（t为参数），定点P（1，1）．
    （Ⅰ）以原点O为极点，x轴的非负半轴为极轴，单位长度与平面直角坐标系下的单位长度相同建立极坐标系，求圆C的极坐标方程；
    （Ⅱ）已知直线l与圆C相交于A，B两点，求||PA|-|PB||的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

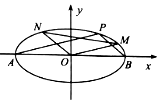    11．已知A，B分别为椭圆C：$\frac{x^2}{4}+\frac{y^2}{2}=1$的左、右顶点，P为椭圆C上异于A，B两点的任意一点，直线PA，PB的斜率分别记为k1，k2．
    （1）求k1k2；
    （2）过坐标原点O作与直线PA，PB平行的两条射线分别交椭圆C于点M，N，问：△MON的面积是否为定值？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．下表是某校高三一次月考5个班级的数学、物理的平均成绩：
    班级12345
    数学（x分）111113119125127
    物理（y分）92939699100
    （Ⅰ）一般来说，学生的物理成绩与数学成绩具有线性相关关系，根据上表提供的数据，求两个变量x，y的线性回归方程$\hat y=\hat bx+\hat a$；
    （Ⅱ）从以上5个班级中任选两个参加某项活动，求至少有一个班级数学平均分在115分以上的概率．
    附：$\hat b=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

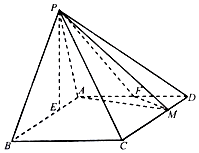    8．在四棱锥P-ABCD中，底面ABCD为平行四边形，AB=3，AD=2$\sqrt{2}$，∠ABC=45°，P点在底面ABCD内的射影E在线段AB上，且PE=2，BE=2EA，F为AD的中点，M在线段CD上，且CM=λCD．
    （Ⅰ）当λ=$\frac{2}{3}$时，证明：平面PFM⊥平面PAB；
    （Ⅱ）当平面PAM与平面ABCD所成的二面角的正弦值为$\frac{{2\sqrt{5}}}{5}$时，求四棱锥P-ABCM的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知向量$\overrightarrow m=（2acosx，sinx）$，$\overrightarrow n=（cosx，bcosx）$，函数$f（x）=\overrightarrow m•\overrightarrow n-\frac{{\sqrt{3}}}{2}$，函数f（x）在y轴上的截距为$\frac{{\sqrt{3}}}{2}$，与y轴最近的最高点的坐标是$（\frac{π}{12}，1）$．
    （Ⅰ）求函数f（x）的解析式；
    （Ⅱ）将函数f（x）的图象向左平移φ（φ＞0）个单位，再将图象上各点的纵坐标不变，横坐标伸长到原来的2倍，得到函数y=sinx的图象，求φ的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．某保险公司针对企业职工推出一款意外险产品，每年每人只要交少量保费，发生意外后可一次性获赔50万元．保险公司把职工从事的所有岗位共分为A、B、C三类工种，根据历史数据统计出三类工种的每赔付频率如下表（并以此估计赔付概率）．
    工种类别ABC
    赔付频率$\frac{1}{1{0}^{5}}$$\frac{2}{1{0}^{5}}$$\frac{1}{1{0}^{4}}$
    （Ⅰ）根据规定，该产品各工种保单的期望利润都不得超过保费的20%，试分别确定各类工种每张保单保费的上限；
    （Ⅱ）某企业共有职工20000人，从事三类工种的人数分布比例如图，老板准备为全体职工每人购买一份此种保险，并以（Ⅰ）中计算的各类保险上限购买，试估计保险公司在这宗交易中的期望利润．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．执行如图所示的程序框图，则输出的k=（　　）
    A．7B．8C．9D．10

    查看答案和解析>>

    同步练习册答案