
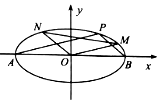
 已知A,B分别为椭圆C:$\frac{x^2}{4}+\frac{y^2}{2}=1$的左、右顶点,P为椭圆C上异于A,B两点的任意一点,直线PA,PB的斜率分别记为k1,k2.
已知A,B分别为椭圆C:$\frac{x^2}{4}+\frac{y^2}{2}=1$的左、右顶点,P为椭圆C上异于A,B两点的任意一点,直线PA,PB的斜率分别记为k1,k2.分析 (1)根据题意,设P(x0,y0),由此表示k1k2,结合椭圆的标准方程分析可得答案;
(2)设M(x1,y1),N(x2,y2),结合(1)的结论可得S的表达式,联立直线与椭圆的位置关系,可得x1、x2的值,将其代入S的表达式,化简变形即可得答案.
解答 解:(1)设P(x0,y0),
则${k_1}{k_2}=\frac{y_0}{{{x_0}+2}}•\frac{y_0}{{{x_0}-2}}=\frac{{{y_0}^2}}{{{x_0}^2-4}}=\frac{{{y_0}^2}}{{-2{y_0}^2}}=-\frac{1}{2}$;
(2)由题知,直线OM:y=k1x,直线ON:y=k2x,
设M(x1,y1),N(x2,y2),
则$S=\frac{1}{2}|{x_1}{y_2}-{x_2}{y_1}|=\frac{1}{2}|{x_1}•{k_2}{x_2}-{x_2}•{k_1}{x_1}|=\frac{1}{2}|({k_1}-{k_2}){x_1}{x_2}|$,
由$\left\{\begin{array}{l}{x^2}+2{y^2}=4\\ y={k_1}x\end{array}\right.⇒{x_1}^2=\frac{4}{{1+2{k_1}^2}}$,
同理可得${x_2}^2=\frac{4}{{1+2{k_2}^2}}$,
故有$4{S^2}={({k_1}-{k_2})^2}•\frac{4}{{1+2{k_1}^2}}•\frac{4}{{1+2{k_2}^2}}=\frac{{16({k_1}^2+{k_2}^2-2{k_1}{k_2})}}{{4{k_1}^2{k_2}^2+2({k_1}^2+{k_2}^2)+1}}$,
又${k_1}{k_2}=-\frac{1}{2}$,故$4{S^2}=\frac{{16({k_1}^2+{k_2}^2+1)}}{{2+2({k_1}^2+{k_2}^2)}}=8$,
∴$S=\sqrt{2}$.
点评 本题考查直线与椭圆的位置关系,涉及椭圆的几何性质,解(1)时要充分利用椭圆的标准方程.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:选择题
| A. | y=2x2 | B. | y=4x2 | C. | y=6x2 | D. | y=8x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | 2π | ||
| C. | 4π | D. | 与点B'的位置有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{44}{45}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{41}{45}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com