
分析 由已知及三角形面积公式可求c2=$\sqrt{2}$sinC,利用余弦定理可求a2+b2=$\sqrt{2}$sinC+2$\sqrt{2}$cosC,利用三角函数恒等变换的应用可求a2+b2+c2=4sin(C+$\frac{π}{4}$),利用正弦函数的有界性即可求得a2+b2+c2的最大值.
解答 解:∵$S=\frac{1}{2}{c^2}$=$\frac{1}{2}$absinC,$ab=\sqrt{2}$,
∴c2=$\sqrt{2}$sinC,
∴$\sqrt{2}$sinC=a2+b2-2abcosC,可得:a2+b2=$\sqrt{2}$sinC+2$\sqrt{2}$cosC,
∴a2+b2+c2=$\sqrt{2}$sinC+2$\sqrt{2}$cosC+$\sqrt{2}$sinC=2$\sqrt{2}$×$\sqrt{2}$($\frac{\sqrt{2}}{2}$sinC+$\frac{\sqrt{2}}{2}$cosC)=4sin(C+$\frac{π}{4}$)≤4,
即a2+b2+c2的最大值是4.
故答案为:4.
点评 本题主要考查了三角形面积公式,余弦定理,三角函数恒等变换的应用,正弦函数的有界性在解三角形中的应用,考查了转化思想,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
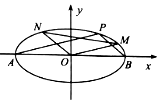 已知A,B分别为椭圆C:$\frac{x^2}{4}+\frac{y^2}{2}=1$的左、右顶点,P为椭圆C上异于A,B两点的任意一点,直线PA,PB的斜率分别记为k1,k2.
已知A,B分别为椭圆C:$\frac{x^2}{4}+\frac{y^2}{2}=1$的左、右顶点,P为椭圆C上异于A,B两点的任意一点,直线PA,PB的斜率分别记为k1,k2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
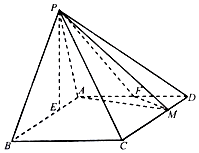 在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,AD=2$\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.
在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,AD=2$\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
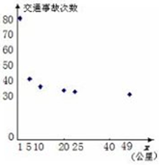 经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:
经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:| 界桩公里数 1001 | 1005 | 1010 | 1020 | 1025 | 1049 |
| 交通事故数 80 | 40 | 35 | 33 | 32 | 30 |
| $\overline{y}$ $\sum_{i=1}^{6}({y}_{i}-\overline{y})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-{\widehat{{y}_{i}}}^{(1)})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-{\widehat{{y}_{i}}}^{(2)})^{2}$ |
| 41.7 1821 | 0.875 | 48.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com