
| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
分析 由已知函数解析式可得f(x)+f(-x)=6,结合f(x)在区间[-k,k](k>0)上的值域为[m,n],即无论k取什么样的正实数都应有最大值与最小值的和是一个确定的值,令k=1得答案.
解答 解:∵$f(x)=3+\frac{{{2^x}-1}}{{{2^x}+1}}+sin2x$,
∴f(-x)=3+$\frac{{2}^{-x}-1}{{2}^{-x}+1}+sin(-2x)$=3-$\frac{{2}^{x}-1}{{2}^{x}+1}-sin2x$,
∴f(x)+f(-x)=6.①
又f(x)在区间[-k,k](k>0)上的值域为[m,n],
即无论k取什么样的正实数都应有最大值与最小值的和是一个确定的值,
故可令k=1,由于函数$f(x)=3+\frac{{{2^x}-1}}{{{2^x}+1}}+sin2x$在区间[-k,k](k>0)上是一个增函数,
故m+n=f(k)+f(-k)
由①知,m+n=f(k)+f(-k)=6.
故选:D.
点评 本题考查函数的值域,考查函数的奇偶性与单调性的性质,属中档题.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | Sn=2n-1 | B. | Sn=2n-1 | C. | Sn=n2 | D. | Sn=2n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
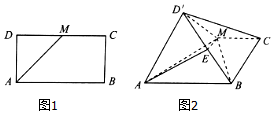 如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.
如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-ln2,0)∪(3,+∞) | B. | (-ln2,+∞) | C. | (3,+∞) | D. | (-ln2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
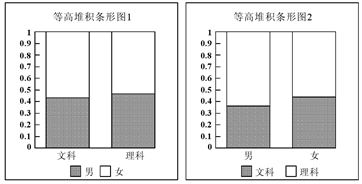
| A. | 样本中的女生数量多于男生数量 | |
| B. | 样本中有理科意愿的学生数量多于有文科意愿的学生数量 | |
| C. | 样本中的男生偏爱理科 | |
| D. | 样本中的女生偏爱文科 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com