
分析 把多项式按乘法展开,将问题转化为二项展开式的系数问题;
利用二项展开式的通项公式求出展开式的通项,
分别令x的指数为3,4求出展开式含x3,x4项的系数;
再求(2x+1)(x-1)5展开式中含x4项的系数.
解答 解:(2x+1)(x-1)5=2x(x-1)5+(x-1)5,
∴(x+2)(x-1)5展开式中含x4项的系数为
(x-1)5展开式中x4系数与x3系数的2倍之和;
∵(x-1)5展开式的通项为Tr+1=(-1)rC5rx5-r,
令5-r=4,得r=1;
∴展开式中含x4的系数为-5;
令5-r=3,得r=2;
∴展开式中含x3的系数为10;
∴(2x+1)(x-1)5展开式中含x4项的系数为
(-5)+2×10=15.
故答案为:15.
点评 本题考查了等价转化的数学思想方法、以及利用二项展开式的通项公式解决二项展开式的特定项问题.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
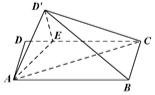 如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
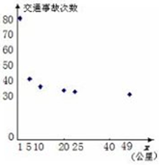 经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:
经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:| 界桩公里数 1001 | 1005 | 1010 | 1020 | 1025 | 1049 |
| 交通事故数 80 | 40 | 35 | 33 | 32 | 30 |
| $\overline{y}$ $\sum_{i=1}^{6}({y}_{i}-\overline{y})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-{\widehat{{y}_{i}}}^{(1)})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-{\widehat{{y}_{i}}}^{(2)})^{2}$ |
| 41.7 1821 | 0.875 | 48.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos2θ | B. | 1 | C. | cos2θ | D. | cos2θ+isinθ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 简单随机抽样 | B. | 系统抽样 | C. | 分层抽样 | D. | 抽签法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费x(万元) | 3 | 4 | 5 | 6 |
| 销售额y(万元) | 25 | 30 | 40 | 45 |
| A. | 73万元 | B. | 73.5万元 | C. | 74万元 | D. | 74.5万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com