
| 广告费x(万元) | 3 | 4 | 5 | 6 |
| 销售额y(万元) | 25 | 30 | 40 | 45 |
| A. | 73万元 | B. | 73.5万元 | C. | 74万元 | D. | 74.5万元 |
科目:高中数学 来源: 题型:选择题
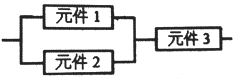 某个部件由三个元件按图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作(其中元件1,2,3正常工作的概率都为$\frac{1}{2}$),设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )
某个部件由三个元件按图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作(其中元件1,2,3正常工作的概率都为$\frac{1}{2}$),设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
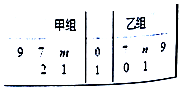 某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$或$-\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$或-$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
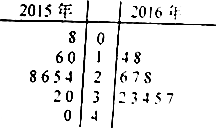 随机抽取某篮球运动员2015年和2016年各10场篮球赛投篮得分X,得到如图所示X的茎叶图.$\overline{X}$2015、$\overline{X}$2016与S22015、S22016是分别是2015年和2016年X的平均数与方差,由图可知( )
随机抽取某篮球运动员2015年和2016年各10场篮球赛投篮得分X,得到如图所示X的茎叶图.$\overline{X}$2015、$\overline{X}$2016与S22015、S22016是分别是2015年和2016年X的平均数与方差,由图可知( )| A. | $\overline{X}$2015>$\overline{X}$2016,S22015>S22016 | B. | $\overline{X}$2015>$\overline{X}$2016,S22015<S22016 | ||
| C. | $\overline{X}$2015<$\overline{X}$2016,S22015<S22016 | D. | $\overline{X}$2015<$\overline{X}$2016,S22015>S22016 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com