
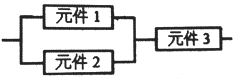
 某个部件由三个元件按图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作(其中元件1,2,3正常工作的概率都为$\frac{1}{2}$),设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )
某个部件由三个元件按图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作(其中元件1,2,3正常工作的概率都为$\frac{1}{2}$),设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{8}$ |
分析 由已知得三个电子元件的使用寿命超过1000小时的概率为p=$\frac{1}{2}$,设A={超过1000小时时,元件1、元件2至少有一个正常},B={超过1000小时时,元件3正常},C={该部件的使用寿命超过1000小时},则P(A)=1-(1-$\frac{1}{2}$)2=$\frac{3}{4}$,P(B)=$\frac{1}{2}$,P(C)=P(AB)=P(A)P(B),由此能求出该部件的使用寿命超过1000小时的概率.
解答 解:∵三个电子元件的使用寿命均服从正态分布N(1000,502),
∴三个电子元件的使用寿命超过1000小时的概率为p=$\frac{1}{2}$,
设A={超过1000小时时,元件1、元件2至少有一个正常},
B={超过1000小时时,元件3正常},
C={该部件的使用寿命超过1000小时},
则P(A)=1-(1-$\frac{1}{2}$)2=$\frac{3}{4}$,P(B)=$\frac{1}{2}$,
故该部件的使用寿命超过1000小时的概率P(C)=P(AB)=P(A)P(B)=$\frac{3}{4}×\frac{1}{2}$=$\frac{3}{8}$.
故选:D.
点评 本题考查概率的求法,考查推理论证能力、运算求解能力,考查化归转化思想、函数与方程思想,是基础题.


科目:高中数学 来源: 题型:解答题
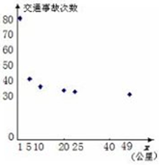 经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:
经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:| 界桩公里数 1001 | 1005 | 1010 | 1020 | 1025 | 1049 |
| 交通事故数 80 | 40 | 35 | 33 | 32 | 30 |
| $\overline{y}$ $\sum_{i=1}^{6}({y}_{i}-\overline{y})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-{\widehat{{y}_{i}}}^{(1)})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-{\widehat{{y}_{i}}}^{(2)})^{2}$ |
| 41.7 1821 | 0.875 | 48.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 26 | B. | 24 | C. | 20 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费x(万元) | 3 | 4 | 5 | 6 |
| 销售额y(万元) | 25 | 30 | 40 | 45 |
| A. | 73万元 | B. | 73.5万元 | C. | 74万元 | D. | 74.5万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x0+△x) | B. | f(x0)+△x | C. | f(x0)•△x | D. | f(x0+△x)-f(x0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,约束条件为$\left\{\begin{array}{l}{y≤-\frac{1}{4}x+\frac{13}{4}}\\{y≥-x+4}\\{y≥\frac{1}{2}x-\frac{1}{2}}\end{array}\right.$,若在可行域△ABC上有无穷多个点(x,y),使得目标函数z=x+my取得最小值,求m的值.
如图,约束条件为$\left\{\begin{array}{l}{y≤-\frac{1}{4}x+\frac{13}{4}}\\{y≥-x+4}\\{y≥\frac{1}{2}x-\frac{1}{2}}\end{array}\right.$,若在可行域△ABC上有无穷多个点(x,y),使得目标函数z=x+my取得最小值,求m的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com